Per la versione in Italiano: https://www.stradeeautostrade.it/ambiente-e-territorio/unanalisi-probabilistica-per-la-stabilita-di-scarpate-secondo-rlem-prima-parte/
Part 2, published on issue n. 141 May/June 2020, is online https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-2/.
Slide2 is one of the most powerful, user friendly, 2D Slope Stability programs in the world. The software is used for evaluating the safety factor or probability of failure of circular and non-circular failure surfaces in soil or rock slopes.
Using the Limit Equilibrium Method (LEM), Slide2 can be used for analyzing both simple and complex models including all types of soil and rock slopes, embankments, earth dams, and retaining walls.
The power of Slide2 comes from its dynamic range of analytical and design options, including built-in finite element groundwater seepage analysis, probabilistic analysis, multi-scenario modeling, and support design.
This wide range of options allows Slide2 users to model complex scenarios with more accurate results.
For example, Slide2 has the capability to consider spatial variability of material properties in your limit equilibrium analysis. The program was actually used to demonstrate the importance of considering spatial variability in the paper Full and quasi-Stochastic Slope Stability Analyses using Random Limit Equilibrium Method (RLEM).
If all of that weren’t enough, with the addition of Maintenance +, Slide2 continues to get even better. Several exciting new features have recently been added to the program this year including a new faster sampling method added for probabilistic analysis called Response Surface, a batch printing feature when doing multi scenario modelling, a new Report Generator, and a new built in list of common support products including geosynthetics, soil nails, and ground anchors.
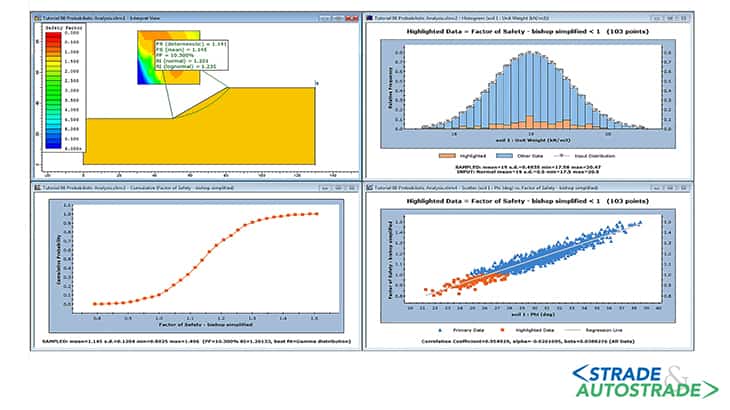
Introduction to the paper
Natural alluvial deposits exhibit variability in strength and deformation parameters due to changes in deposition conditions and processes.
Spatial variability of the strength and stiffness parameters are reflected in the form of uncertainty in stability predictions of the geotechnical structures. Sloped grounds are especially prone to instability due to mobilized static shear stresses.
Innumerable studies have been reported in the literature around the slope stability problem adopting different analysis techniques.
Chronologically, the so-called “approximate” analysis methods precede more cumbersome and complex numerical analysis methods. Although the numerical methods have almost superseded the approximate approaches, these methods have recently proven to be still attractive in some circumstances.
Among all, limit equilibrium method (LEM) of analysis is the most popular approximate approach which is widely employed by researchers to elaborate on the slope stability problems.
Within the stochastic soil mechanics perspective, both numerical and approximate methods have long been invoked to investigate the uncertainty embedded in stability of geo-structures.
Stochastic numerical methods-based analyses of slope stability have a rich history in the technical literature. In [1, 2, 3, 4, 5, 6 and 7] there are many published studies. Random Limit Equilibrium Method (RLEM) has been well-established as a methodology to tackle the difficulty of stochastic stability analysis.
Conventional Limit Equilibrium Method (LEM) in combination with Monte Carlo (MC) simulations has been used extensively by many researchers to interpret the uncertainty embedded in the slope stability analyses assuming both circular and non-circular slip surfaces.
In [8, 9, 10, 11 and 12] there are circular slip surface assumptions in their RLEM analyses. Recently, with the advent of the new search and optimization techniques like Cuckoo search, simulated annealing, auto refine search, block search, path search, Particle Swarm Optimization (PSO), and Surface Altering Optimization (SAO) as discussed by [13, 14, 15, 16 e 17] endeavored to seek for non-circular failure surfaces, necessitated by the fact that circular RLEM could not capture irregular shapes of failure.
This is especially significant when highly fluctuating random fields are encountered. [10] attempted to address some potential advantages of 2D Random Finite Element Method (RFEM) over 1D and 2D circular RLEM analyses for simple cohesive slopes with spatial variability of soil properties.
However, the priority of the RFEM method was argued to be outshined by the massive computational effort embedded in the strength reduction technique.
This paper is an endeavor to elaborate on the potential applications of RLEM in slope stability analyses, by adopting both circular and non-circular failure surfaces when spatially variable soil parameters are encountered in a cohesive-frictional simple slope.
For this reason, 2D RLEM slope stability analysis results for both circular and non-circular slip surface assumptions are compared with a recent 1D RLEM study [11], which sought to map spatially variable fields along a deterministic 1D failure surface.
Furthermore, a so-called quasi-RLEM approach was introduced to simply map the 2D spatially variable strength fields onto the deterministically most probable slip surface. The so-called quasi-RLEM approach could be considered as an alternative to the 1D approach.
Stochastic slope stability analysis
The current study elaborates on the comparative performance of circular and non-circular failure surface assumptions by taking into account the spatial variability of soil parameters. A model with a simple geometry used by [11] is also used in this study.
Before proceeding to the main stochastic analyses, a sensitivity analysis was carried out to make a sound and seamless selection of sufficient number of realizations for subsequent circular and non-circular RLEM analyses.
Four different limit equilibrium approaches namely the Simplified Bishop method, the Morgenstern-Price method, the Spencer method and also the Simplified Janbu method were opted for this purpose. The stochastic properties of the model parameters have been introduced in Figure 2.
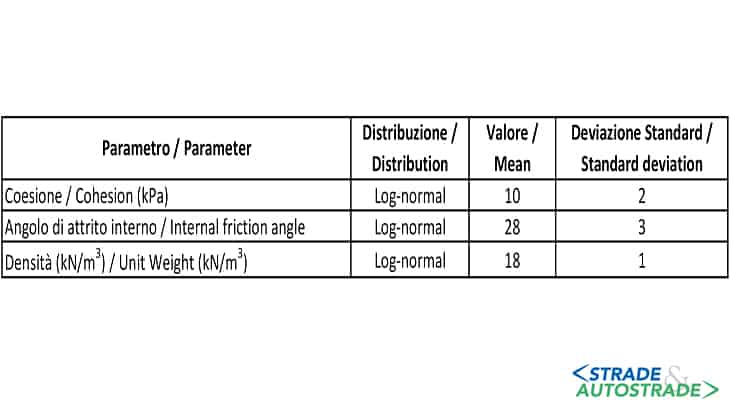
These parameters have been adapted from [11]. However, the only difference is that a log-normal probability distribution function has been opted for the strictly non-negative soil parameters instead of the normal distribution as adopted by [11].
For the sensitivity analyses, no cross-correlation was assumed. However, for the rest of the RLEM analyses a negative cross-correlation coefficient of -0.5 was assumed between the cohesion and the internal friction angle of the soil. On the contrary, the cohesion was assumed positively correlated to the soil unit weight.
A medium cross-correlation coefficient of 0.25 was used in this case. A sensitivity analysis was done in this study and it is observed that adopting 1.000 realizations suffices to capture the underlying stochastic behavior of the spatially variable slope.
Findings of [17] endorses this study by pointing out that only 1.000 Monte Carlo (MC) realizations were needed to generate a stable estimate of the probability of failure through RLEM analyses.
In what follows, three different RLEM approaches will be used in order to compare the different schemes while adopting four well-known slice-based limit equilibrium formulations.
Among the four selected methods, the Simplified Bishop method was ignored for non-circular RLEM analyses because it is very sensitive to the center of the failure zone and in the non-circular analysis it was believed to potentially yield wrong and inappropriate results.
The program Slide2 2018 [18] was used to carry out all the circular and non-circular analyses.
Random circular limit equilibrium
A combination of the classic LEM slope stability analysis together with MC simulations and random field theory was adopted using four different slice-based LEM slope stability formulations as introduced earlier.
For this aim, in each MC simulation, soil parameters were realized through the use of the random field theory and the LAS method which seek to generate spatially variable and correlated stochastic soil parameters.
The realized strength parameters and the stochastic unit weight were then mapped onto the LEM mesh for the stability analysis purposes.
An auto refine search method was used to find the critical circular slip surface corresponding to the minimum factor of safety for each set of random field mesh elements.
All vertical slices are assigned with random soil property values with their base midpoint coinciding with that specific element.
A total of 20 slices was selected by default and deemed sufficient to yield fairly accurate probabilities of failure within sensible computational efforts for all sets of stochastic soil parameters in this investigation.
The slice sensitivity analysis of [17] revealed that for different correlation lengths, increasing the number of slices gave rise to lower probabilities of failure values but at a diminishing rate.
Stochastic non-circular limit equilibrium
In circular slip surface algorithms, the failure state corresponds to a circular failure surface along which a minimum factor of safety is obtained.
However, in spatially variable soil media, circular surfaces will presumably fail to pass through the true weakest points. Therefore, a non-circular surface, represented in its simplest form by a linear spline curve, can be adopted to capture the true failure mechanism of heterogeneous slopes.
For this reason, x and y coordination of some control points will form the optimization input. Surface Altering Optimization (SAO), lying within the family of metaheuristic searching algorithms inspired by nature [19], lends itself to be made in a stepwise computational algorithm to carry out this modification to minimize the factor of safety while averting non-convex geometries and a non-overlapping collection of control points.
Several iterations in forms of repetitive steps are accomplished until convergence criteria are satisfied. An essential factor in SAO is that the entire surface geometry is covered, such that perturbations in coordinates of any control point have impacts on the rearrangement of the other points to maintain convexity of the failure surface and to preserve the initial sequence of the points along the slip surface.
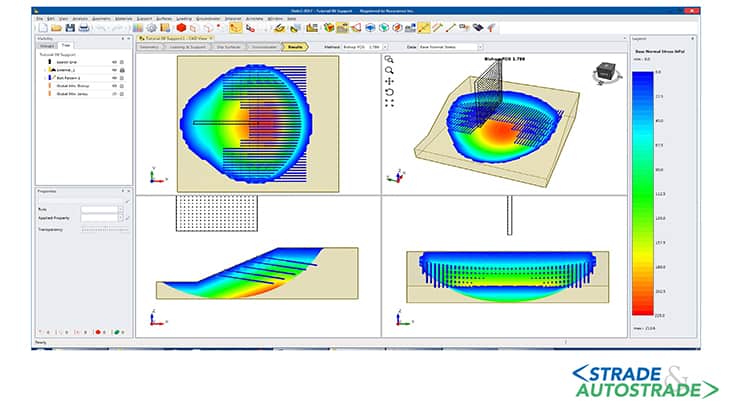
Therefore, the mission of locating a roughly estimated geometry and arrangement of the slip surface with minimum factor of safety lies with the global search method, the Cuckoo search algorithm in this study; the SAO technique simply alters the geometry of the roughly optimized failure surface for further refinement of the factor of safety minimization.
Brute force techniques like the grid search algorithm which has long been utilized in circular slip surface optimizations, might not be efficient for spatially variable soil properties cases.
In [13] the efficiency of rigorous optimization techniques like SAO can be best evaluated when computationally intensive problems such as the stochastic slope stability analysis is considered.
Bibliography
[1]. J.R. Chenari, R. Alaie – “Effect of the heterogeneity of undrained shear strength on the stability of natural slopes”, Sharif Journal of Science and Research, 29 (2), 13-22, 2012
[2]. J.R. Chenari, K.H. Farahbakhsh, M. Zamanzadeh – “Investigation into the effect of the inherent heterogeneity of soil on the long-term stability of earth slopes”, Sharif Journal of Science and Research, 31.2 (3.1), 3-17, 2015.
[3]. J.R. Chenari, R. Alaie – “Effects of anisotropy in correlation structure on the stability of an undrained clay slope”, Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 9(2), 109-123, 2015.
[4]. J.R. Chenari, M. Zamanzadeh – “Uncertainty assessment of critical excavation depth of vertical unsupported cuts in undrained clay using random field theorem. Scientia Iranica. Transaction A, Civil Engineering, 23(3), 864, 2016.
[5]. N. Luo, R.J. Bathurst, S. Javankhoshdel – “Probabilistic stability analysis of simple reinforced slopes by finite element method”, Computers and Geotechnics, 77, 45-55, 2016.
[6]. S. Javankhoshdel, N. Luo, R.J. Bathurst – “Probabilistic analysis of simple slopes with cohesive soil strength using RLEM and RFEM”, Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 11(3), 231-246, 2017.
[7]. J.R. Chenari, R., Kamyab Farahbakhsh, H., & Izadi, A. – “Continuous Slip Surface Method for Stability Analysis of Heterogeneous Vertical Trenches. Scientia Iranica, https://doi.org/ 10.24200/SCI.2019.21227, 2019.
[8]. S. Javankhoshdel, R.J. Bathurst – “Simplified probabilistic slope stability design charts for cohesive and cohesive-frictional (c-ϕ) soils”, Canadian Geotechnical Journal, 51(9), 1033-1045, 2014.
[9]. S. Javankhoshdel, R.J. Bathurst – “Influence of cross correlation between soil parameters on probability of failure of simple cohesive and c-ϕ slopes”, Canadian Geotechnical Journal, 53(5), 839-853, 2015.
[10]. S. Javankhoshdel, B. Cami, R.J. Bathurst, T. Yacoub, B. Corkum – “Probabilistic analysis of cohesive-frictional slopes using the RLEM (circular and con-circular) and the RFEM”, in Proceedings of 70th Canadian Geotechnical Conference, Ottawa, Canada, September 2017.
[11]. A. Johari, S. Mousavi – “An analytical probabilistic analysis of slopes based on limit equilibrium methods”, Bulletin of Engineering Geology and the Environment, 1-15, 2018.
[12]. J.R. Chenari, A. Izadi – “Discussion of “An analytical probabilistic analysis of slopes based on limit equilibrium methods”, by A. Johari, S. Mousavi, November 2018, Bulletin of Engineering Geology and the Environment, 1-5, 2019.
[13]. S. Javankhoshdel, B. Cami, R. Mafi, T. Yacoub, R.J. Bathurst – “Optimization techniques in non-circular probabilistic slope stability analysis considering spatial variability”, in GeoEdmonton 2018, Edmonton, AB, Canada, September 2018, 2018a.
[14]. M. Tabarroki, F. Ahmad, R. Banaki, S.K. Jha, J. Ching – “Determining the factors of safety of spatially variable slopes modeled by random fields”, Journal of Geotechnical and Geoenvironmental Engineering, 139(12), 2082-2095, 2013.
[15]. B. Cami, S. Javankhoshdel, J. Lam, R.J. Bathurst, T. Yacoub – “Probabilistic analysis of a tailings dam using 2d composite circular and non-circular deterministic analysis”, SRV Approach, and RLEM, in Proceedings of 70th Canadian Geotechnical Conference, Ottawa, Canada, September 2017.
[16]. S. Javankhoshdel, B. Cami, R.J. Bathurst, B. Corkum – “Probabilistic analysis of layered slopes with linearly increasing cohesive strength and 2D spatial variability of soil strength parameters using non-circular RLEM approach”, in IFCEE 2018, pp. 133-142, 2018b.
[17]. B. Cami, S. Javankhoshdel, R.J. Bathurst, T. Yacoub – “Influence of mesh size, number of slices, and number of simulations in probabilistic analysis of slopes considering 2D spatial variability of soil properties”, in IFCEE 2018, pp. 186-196.
[18]. Rocscience Inc. 2018. Slide2 Version 2018-2D Limit Equilibrium Slope Stability Analysis, www.rocscience.com, Toronto, Ontario, Canada.
[19]. A.H. Gandomi, A.R. Kashani, M. Mousavi, M. Jalalvandi – “Slope stability analysis using evolutionary optimization techniques”, International Journal for Numerical and Analytical Methods in Geomechanics, 41(2), 251-264, 2017.
Part 2, published on issue n. 141 May/June 2020, is online https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-2/.
Per la versione in Italiano: https://www.stradeeautostrade.it/ambiente-e-territorio/unanalisi-probabilistica-per-la-stabilita-di-scarpate-secondo-rlem-prima-parte/