![]() For English version: https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-1/
For English version: https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-1/
La seconda parte, proposta su “S&A” n° 141 Maggio/Giugno 2020, è online https://www.stradeeautostrade.it/ambiente-e-territorio/unanalisi-probabilistica-per-la-stabilita-di-scarpate-secondo-rlem-seconda-parte/.
Slide2 è uno dei programmi di stabilità di scarpate e pendii più potenti e intuitivi al mondo. Il software viene utilizzato per valutare il fattore di sicurezza o la probabile instabilità di superfici circolari e non circolari in terreni o pendii rocciosi.
Utilizzando il metodo dell’equilibrio limite (LEM), Slide2 può essere utilizzato per analizzare modelli sia semplici che complessi, considerando tutti i tipi di terreno e pendii rocciosi, argini, dighe in terra, muri di contenimento, ancoraggi e altro ancora.
La potenza di Slide2 deriva dalla sua ampia gamma di opzioni analitiche e di progettazione che include, ad esempio, l’analisi di fenomeni di fitrazione agli elementi finiti, analisi probabilistica, modellazione multi-scenario e progettazione elementi di supporto (come geosintetici o soil nailing).
Questa vasta gamma di opzioni consente agli utenti di Slide2 la modellazione di scenari complessi con risultati più accurati e veloci.
Ad esempio, Slide2 ha la capacità di considerare la variabilità spaziale delle proprietà dei materiali nell’analisi dell’equilibrio limite. Nell’articolo che segue si evidenzia come il programma sia stato utilizzato con successo per dimostrare l’importanza della variabilità spaziale nella progettazione.
Se tutto ciò non bastasse, con l’aggiunta di Maintenance +, Slide2 continua a migliorare ancora.
Nel 2020, diverse nuove interessanti funzionalità sono state aggiunte al programma: tra queste, il nuovo e più veloce metodo di campionamento per l’analisi probabilistica chiamato “Response Surface”, la funzione di stampa batch per la modellazione multi-scenario, il nuovo generatore di report e la nuova libreria prodotti tra cui geosintetici, soil nailing, barre auto-perforanti e vari ancoraggi in terra.
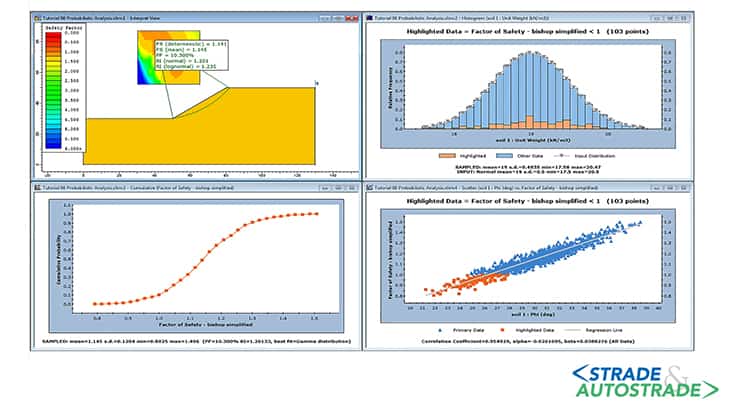
Introduzione al paper
I depositi alluvionali possiedono una grande variabilità nei parametri geotecnici (sforzi e deformazione) a causa dei cambiamenti dovuti alle condizioni e processi di deposizione.
La variabilità spaziale dei parametri geotecnici si riflette in incertezza nelle previsioni della stabilità in strutture geotecniche. I terreni in pendenza poi sono specialmente soggetti a instabilità a causa degli sforzi mobilizzati di taglio.
Molteplici studi, disponibili in letteratura, considerano i problemi di stabilità delle pendenze adottando diversi metodi di calcolo e analisi. Cronologicamente, i metodi di analisi “semplificati” precedono molti metodi numerici di analisi complessi.
Anche se i metodi di analisi numerici hanno ormai preso il posto degli approcci semplificati, questi metodi sono comunque usati e affidabili in certe circostanze.
Tra tutti i metodi “semplificati”, quello all’equilibrio limite (LEM) è sicuramente il più popolare ed usato per elaborare analisi dei problemi di instabilità delle scarpate.
Secondo l’analisi probabilistica della meccanica dei terreni, sia i metodi numerici che semplificati sono stati a lungo impiegati per investigare l’incertezza intrinseca della stabilità delle geostrutture.
Metodi di analisi numerici probabilistici applicati alla stabilità delle scarpate hanno una ricca storia nella letteratura tecnica.
In [1, 2, 3, 4, 5, 6 e 7] si trovano sono solo alcuni dei molti studi pubblicati. Il Random Limit Equilibrium Method (RLEM) ha dimostrato di essere una metodologia valida per affrontare le difficoltà dell’analisi di stabilità probabilistica.
Il metodo all’equilibrio limite (LEM) in combinazione con simulazioni Monte Carlo (MC) è stato usato largamente da molti Ricercatori per interpretare l’incertezza intrinseca nelle analisi di stabilità delle scarpate ammettendo superfici di scorrimento circolari e non circolari. In [8, 9, 10, 11 e 12] sono stati ipotizzate superfici di scorrimento circolari nelle loro RLEM analisi.
Visto che il metodo circolare RLEM non poteva rilevare l’instabilità a scorrimento con forme irregolari (situazione molto significativa specialmente quando si incontrano scenari con alta variabilità), sono state attivate varie ricerche e studi. Recentemente, i nuovi studi e l’ottimizzazione di modelli come Cuckoo search,
simulata “annealing”, ricerca “auto-refine”, Ricerca Blocco, Ricerca Percorso, Particle Swarm Optimization (PSO) e Surface Altering Optimization (SAO) [13, 14, 15, 16 e 17] hanno permesso di studiare i fenomeni di instabilità per superfici non circolari.
[10] tentarono di dimostrare i vantaggi di 2D Random Finite Element Method (RFEM) su 1D e 2D analisi circolari RLEM per scarpate a terreno coesivo con variabilità spaziale delle proprietà del suolo.
Tuttavia, le considerazioni del metodo RFEM sono state messe in discussione dall’enorme impegno computazionale intrinseco nella tecnica di riduzione degli sforzi.
Questo articolo cerca quindi di indagare il potenziale del metodo RLEM nell’analisi di stabilità delle scarpate, adottando superfici di instabilità e scorrimento – sia circolari che non circolari -, considerando le variabili spaziali parametriche per scarpate in terreni coesivi.
Per questa ragione, l’analisi di stabilità delle scarpate 2D RLEM, per ipotesi di superfici di scorrimento circolari e non circolari, sono confrontate con il recente studio 1D RLEM [11], il quale ha cercato di mappare i campi di variabilità spaziale con un’analisi deterministica 1D per le superfici di scorrimento.
Inoltre, il cosiddetto approccio quasi-RLEM è stato introdotto per mappare semplicemente la variabile spaziale 2D dei campi di forza all’interno della più probabile superficie di scorrimento.
Il cosiddetto approccio quasi-RLEM potrebbe essere considerato come un’alternativa dell’approccio 1D.
L’analisi probabilistica di stabilità per scarpate
Questa ricerca vuole confrontare le ipotesi di instabilità per superfici circolari e non circolari, tenendo in considerazione la variabilità spaziale dei parametri del terreno. Un modello a geometria semplice, usato anche in [11], viene utilizzato in questo studio.
Prima di procedere con le principali analisi probabilistiche, è stata condotta un’analisi di sensitività per fare una pre-selezione di un numero sufficiente di casi, da analizzare sucessivamente tramite RLEM circolare e non circolare.
Sono stati scelti per questo studio quattro approcci differenti all’equilibrio limite: il metodo semplificato di Bishop, il metodo Morgenstern-Price, il metodo Spencer e il metodo semplificato di Janbu. Le proprietà probabilistiche dei parametri del modello sono esposti in Figura 2.
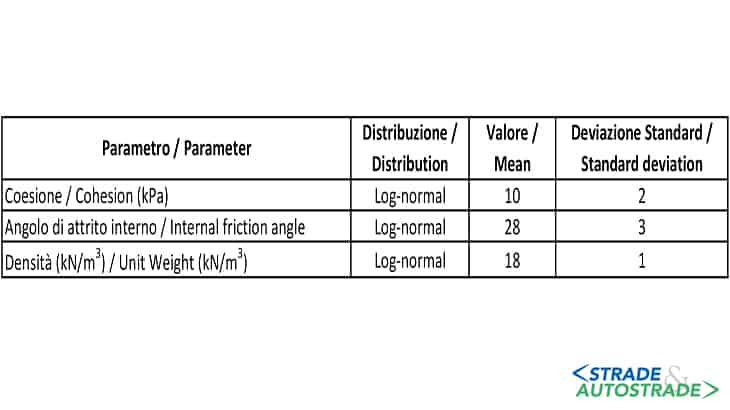
Questi parametri sono stati adottati da [11]. Tuttavia, l’unica differenza è che una funzione logaritmica-normale (log-normal) di probabilità di distribuzione è stata adottata per alcuni parametri del terreno, anzichè una normale distribuzione come ipotizzato [11]. Per le analisi di sensitività, non è stata considerata nessuna intrinseca-correlazione.
Tuttavia, per le analisi RLEM è stato ipotizzato un coefficiente di correlazione incrociata negativo di -0,5 tra la coesione e l’angolo di attrito del terreno.
Al contrario, la coesione è stata ipotizzata positivamente correlata alla densità del terreno. In questo caso è stato utilizzato un coefficiente di correlazione medio di 0,25.
In questo studio è stata condotta un’analisi di sensibilità e si osserva che l’adozione di 1.000 analisi è sufficiente per inquadrare il comportamento stocastico della scarpata spazialmente variabile.
I risultati di [17] sostengono questo studio, sottolineando che sono necessarie solo 1.000 analisi Monte Carlo (MC) per generare una stima stabile della probabilità di instabilità attraverso le analisi RLEM.
Di seguito, verranno utilizzati tre diversi approcci RLEM al fine di confrontare i diversi schemi adottando quattro formule di equilibrio limite basate su conci (slice) ben noti.
Tra i quattro metodi selezionati, il metodo Bishop semplificato è stato ignorato per le analisi RLEM non circolari perché è molto sensibile al centro della zona di instabilità e nell’analisi non circolare si riteneva che potesse produrre risultati errati e inappropriati. Il programma Slide2 (Rocscience) è stato utilizzato per eseguire tutte le analisi circolari e non circolari [18].
L’equilibrio limite circolare casuale
Una combinazione della classica analisi di stabilità della scarpata LEM con simulazioni MC e teoria dei campi casuali è stata adottata usando quattro diverse formulazioni di stabilità della scarpata LEM basate sul concio, come precedentemente introdotto.
A tale scopo, in ciascuna simulazione MC, i parametri del suolo sono stati caratterizzati attraverso l’uso della teoria dei campi casuali e del metodo LAS che cercano di generare parametri del terreno stocastici spazialmente variabili e correlati.
I parametri di resistenza e il peso unitario stocastico del terreno sono stati quindi mappati sulla “mesh” LEM ai fini dell’analisi di stabilità.
È stato utilizzato un metodo di ricerca di perfezionamento automatico (auto-refine) per trovare la superficie di scorrimento circolare critica corrispondente al fattore minimo di sicurezza per ciascun set di elementi di “mesh” di campo casuali.
A tutte le sezioni verticali sono assegnate valori casuali delle proprietà del terreno. Un totale di 20 conci sono stati selezionati e ritenuti sufficienti per produrre un’analisi probabilistica abbastanza accurata.
L’analisi della sensibilità del concio da [17] ha rivelato che per diverse lunghezze di correlazione, l’aumento del numero di sezioni ha dato luogo a probabilità più basse dei valori di instabilità ma a un ritmo decrescente.
L’equilibrio limite non circolare stocastico
Negli algoritmi della superficie di scorrimento circolare, lo stato di errore corrisponde a una superficie di errore circolare lungo la quale si ottiene un fattore minimo di sicurezza.
Tuttavia, nei terreni spazialmente variabili, le superfici circolari presumibilmente non riescono a passare attraverso i veri punti più deboli.
Pertanto, una superficie non circolare, rappresentata nella sua forma più semplice da una curva lineare, può essere adottata per catturare il vero meccanismo di rottura di scarpate eterogenee.
Per questo motivo, il coordinamento x-y con alcuni punti di controllo potrà permettere l’ottimizzazione.
Surface Altering Optimization (SAO), che rientra nella famiglia di algoritmi di ricerca metauristica ispirati dalla natura da [19], si presta ad essere l’algoritmo computazionale per effettuare questa modifica, riducendo al minimo il fattore di sicurezza, evitando geometrie convesse e una raccolta non sovrapposta di punti di controllo.
Diverse iterazioni, con passaggi ripetitivi, vengono eseguite fino a quando non vengono soddisfatti i criteri di convergenza.
Un fattore essenziale in SAO è che l’intera geometria della superficie è coperta, in modo tale che le perturbazioni nelle coordinate di qualsiasi punto di controllo abbiano impatti sulla ridistribuzione degli altri punti per mantenere la convessità della superficie di rottura e preservare la sequenza iniziale dei punti lungo la superficie di scorrimento.
Pertanto, lo scopo di individuare e stimare una geometria e la disposizione della superficie di scorrimento con un fattore di sicurezza minimo risiede nel metodo di ricerca globale, cioè l’algoritmo di ricerca Cuckoo in questo studio.
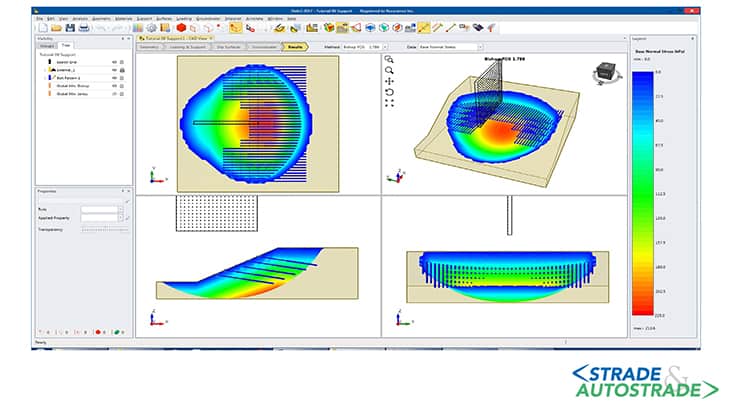
La tecnica SAO altera semplicemente la geometria della superficie di rottura approssimativamente ottimizzata per un ulteriore affinamento del fattore di riduzione della sicurezza.
Tecniche di forzatura dei risultati come l’algoritmo di ricerca della griglia, che è stato a lungo utilizzato nelle ottimizzazioni circolari della superficie di scorrimento, potrebbero non essere efficienti per i casi con proprietà del terreno spazialmente variabili.
In [13] si sostiene che l’efficienza di rigorose tecniche di ottimizzazione come SAO può essere valutata al meglio quando si considerano problemi intensivamente computazionali come l’analisi della stabilità del pendio stocastica.
Bibliografia
[1]. J.R. Chenari, R. Alaie – “Effect of the heterogeneity of undrained shear strength on the stability of natural slopes”, Sharif Journal of Science and Research, 29 (2), 13-22, 2012.
[2]. J.R. Chenari, K.H. Farahbakhsh, M. Zamanzadeh – “Investigation into the effect of the inherent heterogeneity of soil on the long-term stability of earth slopes”, Sharif Journal of Science and Research, 31.2 (3.1), 3-17, 2015.
[3]. J.R. Chenari, R. Alaie – “Effects of anisotropy in correlation structure on the stability of an undrained clay slope”, Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 9(2), 109-123, 2015.
[4]. J.R. Chenari, M. Zamanzadeh – “Uncertainty assessment of critical excavation depth of vertical unsupported cuts in undrained clay using random field theorem. Scientia Iranica. Transaction A, Civil Engineering, 23(3), 864, 2016.
[5]. N. Luo, R.J. Bathurst, S. Javankhoshdel – “Probabilistic stability analysis of simple reinforced slopes by finite element method”, Computers and Geotechnics, 77, 45-55, 2016.
[6]. S. Javankhoshdel, N. Luo, R.J. Bathurst – “Probabilistic analysis of simple slopes with cohesive soil strength using RLEM and RFEM”, Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 11(3), 231-246, 2017.
[7]. J.R. Chenari, R., Kamyab Farahbakhsh, H., & Izadi, A. – “Continuous Slip Surface Method for Stability Analysis of Heterogeneous Vertical Trenches, Scientia Iranica, https://doi.org/ 10.24200/SCI.2019.21227, 2019.
[8]. S. Javankhoshdel, R.J. Bathurst – “Simplified probabilistic slope stability design charts for cohesive and cohesive-frictional (c-ϕ) soils”, Canadian Geotechnical Journal, 51(9), 1033-1045, 2014.
[9]. S. Javankhoshdel, R.J. Bathurst – “Influence of cross correlation between soil parameters on probability of failure of simple cohesive and c-ϕ slopes”, Canadian Geotechnical Journal, 53(5), 839-853, 2015.
[10]. S. Javankhoshdel, B. Cami, R.J. Bathurst, T. Yacoub, B. Corkum – “Probabilistic analysis of cohesive-frictional slopes using the RLEM (circular and con-circular) and the RFEM”, in Proceedings of 70th Canadian Geotechnical Conference, Ottawa, Canada, September 2017.
[11]. A. Johari, S. Mousavi – “An analytical probabilistic analysis of slopes based on limit equilibrium methods”, Bulletin of Engineering Geology and the Environment, 1-15, 2018.
[12]. J.R. Chenari, A. Izadi – “Discussion of “An analytical probabilistic analysis of slopes based on limit equilibrium methods”, by A. Johari, S. Mousavi, November 2018, Bulletin of Engineering Geology and the Environment, 1-5, 2019.
[13]. S. Javankhoshdel, B. Cami, R. Mafi, T. Yacoub, R.J. Bathurst – “Optimization techniques in non-circular probabilistic slope stability analysis considering spatial variability”, in GeoEdmonton 2018, Edmonton, AB, Canada, September 2018, 2018a.
[14]. M. Tabarroki, F. Ahmad, R. Banaki, S.K. Jha, J. Ching – “Determining the factors of safety of spatially variable slopes modeled by random fields”, Journal of Geotechnical and Geoenvironmental Engineering, 139(12), 2082-2095, 2013.
[15]. B. Cami, S. Javankhoshdel, J. Lam, R.J. Bathurst, T. Yacoub – “Probabilistic analysis of a tailings dam using 2d composite circular and non-circular deterministic analysis”, SRV Approach, and RLEM, in Proceedings of 70th Canadian Geotechnical Conference, Ottawa, Canada, September 2017.
[16]. S. Javankhoshdel, B. Cami, R.J. Bathurst, B. Corkum – “Probabilistic analysis of layered slopes with linearly increasing cohesive strength and 2D spatial variability of soil strength parameters using non-circular RLEM approach”, in IFCEE 2018, pp. 133-142, 2018b.
[17]. B. Cami, S. Javankhoshdel, R.J. Bathurst, T. Yacoub – “Influence of mesh size, number of slices, and number of simulations in probabilistic analysis of slopes considering 2D spatial variability of soil properties”, in IFCEE 2018, pp. 186-196.
[18]. Rocscience Inc. 2018. Slide2 Version 2018-2D Limit Equilibrium Slope Stability Analysis, www.rocscience.com, Toronto, Ontario, Canada.
[19]. A.H. Gandomi, A.R. Kashani, M. Mousavi, M. Jalalvandi – “Slope stability analysis using evolutionary optimization techniques”, International Journal for Numerical and Analytical Methods in Geomechanics, 41(2), 251-264, 2017.
La seconda parte, proposta su “S&A” n° 141 Maggio/Giugno 2020, è online https://www.stradeeautostrade.it/ambiente-e-territorio/unanalisi-probabilistica-per-la-stabilita-di-scarpate-secondo-rlem-seconda-parte/.
![]() For English version: https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-1/
For English version: https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-1/
> Se questo articolo ti è piaciuto, iscriviti alla Newsletter mensile al link http://eepurl.com/dpKhwL <

