Full and quasi-stochastic slope stability analysis using random limit equilibrium method (RLEM) – part 2 ![]() Per la versione in Italiano: https://www.stradeeautostrade.it/ambiente-e-territorio/unanalisi-probabilistica-per-la-stabilita-di-scarpate-secondo-rlem-seconda-parte/
Per la versione in Italiano: https://www.stradeeautostrade.it/ambiente-e-territorio/unanalisi-probabilistica-per-la-stabilita-di-scarpate-secondo-rlem-seconda-parte/
Part 1, published on issue n. 141 May/June 2020, is online https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-1/.
1D and quasi-stochastic slope stability
The use of spatially variable analysis affects the calculated probability of failure of slope models.
[1] assert that for slope models with a mean factor of safety greater than 1, accounting for spatial variability of material properties (e.g. cohesion and unit weight) results in a lower probability of failure, compared to the same analysis without using spatial variability.
A probabilistic analysis that does not consider spatial variability has been shown to result in unrealistic and overly conservative probabilities of failure [1].
Conventional 1D random field generation in slope stability problems refers to the realization of stochastic soil parameters along a predetermined and plausible slip surface passing through the soil domain.
This is not believed to yield realistic results as the soil properties are solely realized along a prescribed failure surface which is normally reached by some deterministic analyses adopting the soil parameters in an average sense.
Very recently, [2] compared results of such 1D stochastic analyses with some traditional probabilistic analytical solutions for the slope geometry studied herewith.
Earlier, [1] compared the results of some 2D stochastic slope stability analyses with 1D random field description of the soil parameters as explained above. In [3] also carried out similar 1D stochastic analyses on stability of vertical cuts.
An arguably more viable solution can be provided if instead of simple 1D stochastic modelling, a quasi-stochastic random field description is adopted.
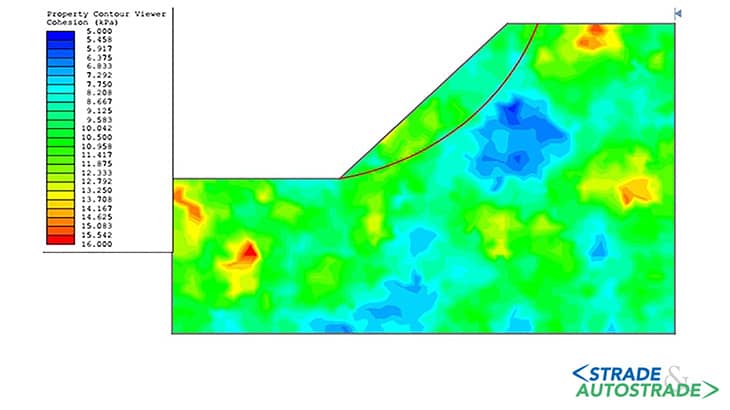
This implies that the spatially variable soil parameters are first realized throughout the 2D domain. Next, the corresponding values across the predetermined slip surface are picked and introduced into slope stability slicebased calculations for each MC simulation.
Figure 1 demonstrates a sample quasi-stochastic slope stability realization along with the assumed slip surface. It is worth mentioning that the prescribed slip surface may bypass the weakest points in some MC simulations as appears in Figure 1.
This circumvention behavior, inherent in quasi-stochastic slope stability calculations, is indeed inevitable; however, when compared to the simple and admittedly nonrealistic 1D approach, it is deemed to outperform it. In what follows, comparative illustrations of the distribution of the safety factor will be provided and discussed accordingly.
As mentioned earlier, Surface Altering optimization was used in this study together with the Cuckoo search method to find the critical factor of safety for each trial calculation.
Results and discussions
Results of MC simulations for different stochastic approaches were furnished in the forms of Probability Distribution Function (PDF) and Cumulative Distribution Function (CDF). Various slicebased slope stability formulations, namely, the Simplified Janbu method, the Spencer method, and the Morgenstern-Price method have been chosen for demonstration purposes, while the results of the Simplified Bishop method were ignored for the reason explained earlier.
The circular and non-circular full stochastic slope stability analyses along with the quasi-stochastic scheme have been presented. The latter is considered as an alternative to the 1D stochastic slope stability analysis.
In general, it is observed that the non-circular stochastic RLEM slope stability approach yields more conservative slope stability evaluations.
This is as expected as in heterogeneous slopes, the non-circular LEM-based formulation is more apt to capture the failure surface passing through the weakest path. It is further noted that the quasi-stochastic RLEM slope stability analyses have rendered the most unconservative predictions of the safety factor in average sense.
According to what was discussed on the sample quasi-stochastic realization presented in Figure 2, this behavior is justifiable as some weak points are prone to be circumvented when a predetermined slip surface is considered in the quasi-stochastic approach.
Overall, the superiority of the non-circular RLEM slope stability approach over the circular approaches is corroborated by comparing the mean safety factors from different approaches.
It is further noted that the so-called quasi-stochastic approach, while rendering non-conservative slope stability analysis results, could be considered as a consistent alternative to the controversial 1D stochastic approach.
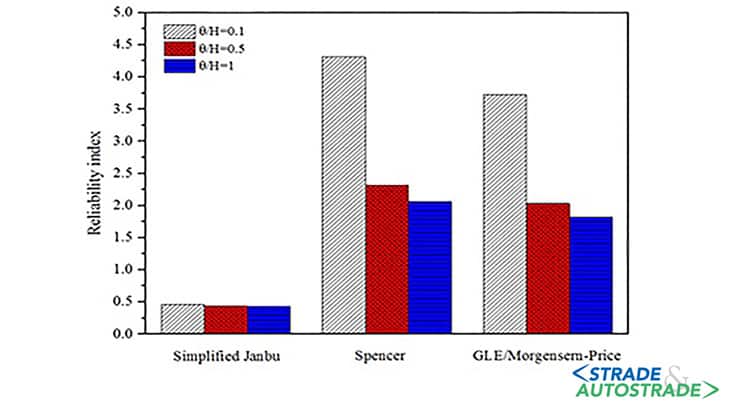
Another observation from the slope stability analysis results is that neglecting the auto-correlation of the strength parameters in non-circular RLEM approach would give unconservative results as endorsed from the reliability charts for different scales of fluctuation (Figure 2).
The reliability index was acquired from linearization of the performance function around the mean value of the safety factor representing a random variable in FOSM approach. The performance function was adopted as M = FS – 1 and the reliability index was estimated through β = (μ (FS) – 1) / (σ (FS)).
Comparing the CDF curves vertically for different scales of fluctuation can also lead to conclusions about the impact of the scale of fluctuation on the reliability index of the slope stability analyses.
Although the differences between the mean safety factors corresponding to different scales of fluctuation are not quite discernible, the more flatter CDF curves in the largest scale of fluctuation lends support to the contention that increasing the scale of fluctuation brings about a reduced reliability.
At limit, when a large correlation length is encountered, the circular and quasi-stochastic results almost coincide. In such circumstances, the slope stability analyses are indeed an assembly of random homogeneous cases which converge in average to the deterministic solution.
The results in such a condition should normally be comparable with the probabilistic responses of [2]. CDF curves are good to show the consistency in these specific cases.
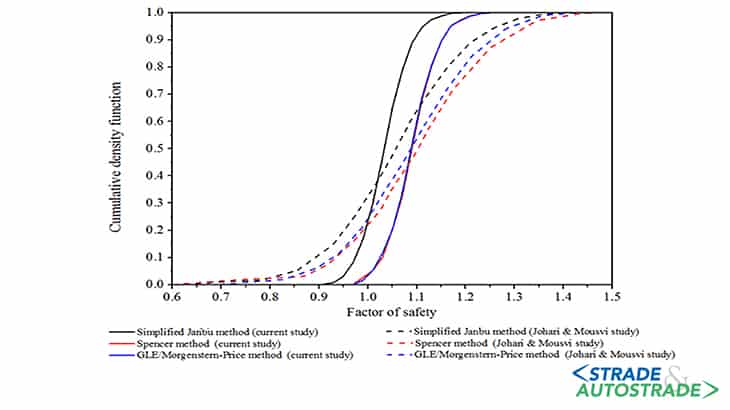
However, as illustrated in Figure 3, the results of the circular full stochastic RLEM analyses for the large scale of fluctuation are not in close conformity to the results of the probabilistic analyses reported by [2].
Although the results are in good agreement in terms of the mean values, it seems that the variability of the safety factor data is not of the same structure. The discrepancy can be attributed to the difference in the probability distribution function between the two studies.
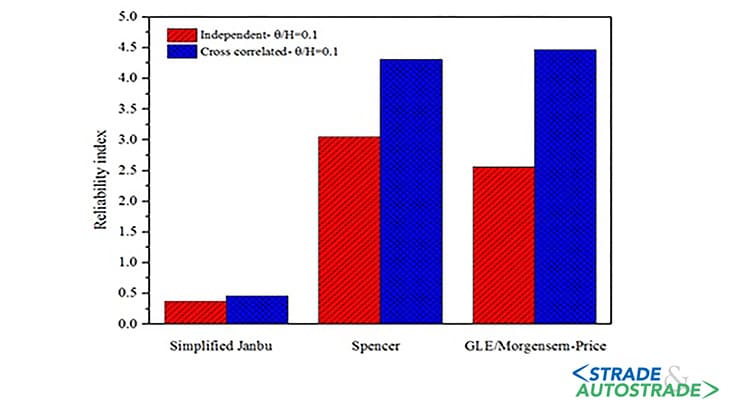
Furthermore, it was shown that overlooking the cross-correlation between the strength parameters in slope stability problems may give rise to conservative results.
This can be supported by illustrating the reliability index charts of the cases corresponding to independent and cross-correlated strength parameters for the non-circular stochastic RLEM approach.
Figure 4 clearly indicates that neglecting the negative cross-correlation between the cohesion and the internal friction angle will, due to the augmented chance of weak points formation, lead to increased potential of slope instability.
As the strength parameters are taken negatively correlated, when the cohesion in some elements becomes low, the internal friction angle field generation engine will presumably render high values to comply with the cross-correlation requirements.
Therefore, considering the cross-correlation between the strength parameters is expected to induce a reduction in probability of failure of the heterogeneous slope as appears from Figure 4.
Conclusion
The following conclusions were derived through comparisons of the results of the different RLEM approaches, namely the circular and non-circular full stochastic RLEM approaches, and the quasi-stochastic RLEM block search models.
Non-circular slip surface consideration, due to its versatility in capturing arbitrary failure geometries, proved to be more efficient in detecting the most critical stability conditions in comparison to the traditional slice-based circular algorithms.
It was shown that the non-circular assumption will yield lower factors of safety for the heterogeneous slopes in an average sense.
Overall, the reliability index of the nonhomogeneous slopes, considering the non-circular failure geometry, was indicated to decrease the reliability index of the slope by yielding a higher probability of failure.
It was shown that the quasi-stochastic RLEM analyses render slightly unconservative stability evaluations by returning a higher mean safety factor than the circular/non-circular full stochastic RLEM approaches. However, it is maintained that it can still be a decent alternative to the inaccurate 1D stochastic slope stability approach.
The strength parameters’ auto-correlation structure was shown to have a serious reliability impact on slope stability analyses through adopting the RLEM approaches.
Disregarding the correlation structure of the strength parameters, namely the cohesion and the internal friction angle, will lead to increased reliability indices and therefore an unconservative stability evaluation to be given out.
The negative cross-correlation between the strength parameters proved to have an important influence on the safety factor predictions in an average sense.
It was indicated that neglecting the covariance structure of the multiple strength parameters involved in the stability analysis of heterogeneous slopes will return conservative stability analyses within the reliability-based design perspective.
Bibliography
[1]. S. Javankhoshdel, B. Cami, R.J. Bathurst, T. Yacoub, B. Corkum – “Probabilistic analysis of cohesive-frictional slopes using the RLEM (circular and con-circular) and the RFEM”, in Proceedings of 70th Canadian Geotechnical Conference, Ottawa, Canada, September 2017.
[2]. A. Johari, S. Mousavi – “An analytical probabilistic analysis of slopes based on limit equilibrium methods”, Bulletin of Engineering Geology and the Environment, 1-15, 2018.
[3]. J.R. Chenari, M. Zamanzadeh – “Uncertainty assessment of critical excavation depth of vertical unsupported cuts in undrained clay using random field theorem. Scientia Iranica. Transaction A, Civil Engineering, 23(3), 864, 2016.
Part 1, published on issue n. 141 May/June 2020, is online https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-1/.
![]() Per la versione in Italiano: https://www.stradeeautostrade.it/ambiente-e-territorio/unanalisi-probabilistica-per-la-stabilita-di-scarpate-secondo-rlem-seconda-parte/
Per la versione in Italiano: https://www.stradeeautostrade.it/ambiente-e-territorio/unanalisi-probabilistica-per-la-stabilita-di-scarpate-secondo-rlem-seconda-parte/

