Nel presente articolo sono riportati i risultati delle analisi numeriche effettuate per la progettazione della galleria naturale GN02 Serra Castello, che rientra nell’ambito dei “Lavori di nuova costruzione e parziale adeguamento della strada di collegamento Cosenza-Sibari, nel tratto compreso tra lo svincolo A3 uscita Tarsia e la S.S. 106 bis – 2° Lotto”.
La progettazione è stata effettuata secondo il metodo di Analisi delle Deformazioni Controllate nelle Rocce e nei Suoli (ADECO-RS) sviluppato da Pietro Lunardi [1] e che prevede le seguenti fasi:
- fase conoscitiva comprendente gli studi geologici, le indagini geotecniche, la loro interpretazione e la definizione dei parametri geotecnici per la progettazione delle opere;
- fase di diagnosi nella quale, sulla base delle conoscenze raccolte nella fase conoscitiva, il Progettista fornisce previsioni circa il comportamento tenso-deformativo dell’ammasso a seguito dello scavo della galleria, in assenza di interventi di stabilizzazione;
- fase di terapia nella quale sono definiti gli interventi di stabilizzazione più idonei per controllare le deformazioni attese.
Descrizione del progetto
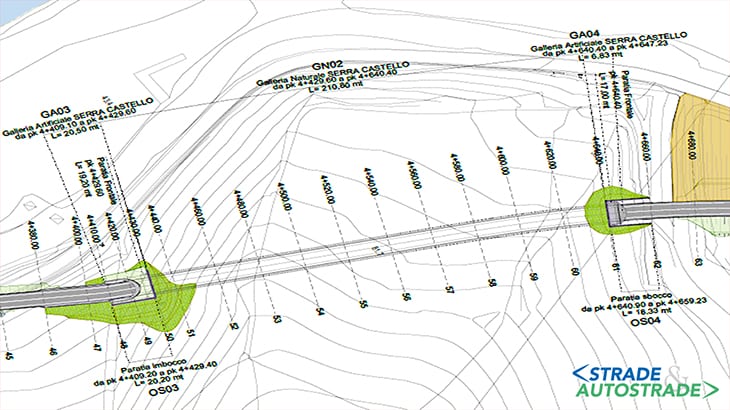
La galleria naturale GN02 Serra Castello si estende tra le p.k. 4+429,60 e 4+640,40 della S.P. 197 per una lunghezza complessiva di 210,80 m (Figura 1 sopra).
La sezione media di scavo è pari a circa 130 m2, con larghezza massima di 14 m e altezza pari a 11,50 m; la massima copertura prevista in chiave calotta risulta approssimativamente pari a 36 m.
La sezione stradale è di tipo C2, con due corsie di marcia da 3,50 m e due banchine da 1,25 m. Il progetto ha previsto l’impiego dei seguenti materiali:
- rivestimenti provvisionali con:
- carpenteria metallica in acciaio tipo S275;
- spritz beton fibrorinforzato, realizzato con calcestruzzo di classe C 28/35;
- rivestimenti definitivi, realizzati con calcestruzzo di classe C 32/40;
- miscele cementizie per lavori di consolidamento con cemento tipo 42.5R, rapporto bentonite/acqua < 0,02 (eventuale) e additivo fluidificante 4% di peso del cemento.
Nel presente studio viene presa in esame la sezione della galleria posizionata alla pk. 4+480 circa, dove si riscontrano le massime coperture in chiave calotta (circa 36 m).
La fase conoscitiva
Da un punto di vista geologico, lo scavo della galleria interessa la Formazione di Diamante, costituita da metabasiti, filladi, scisti filladici e calcescisti. Si tratta di litotipi di natura ofiolitica intensamente piegati e fratturati sia per tettonica compressiva che estensionale.
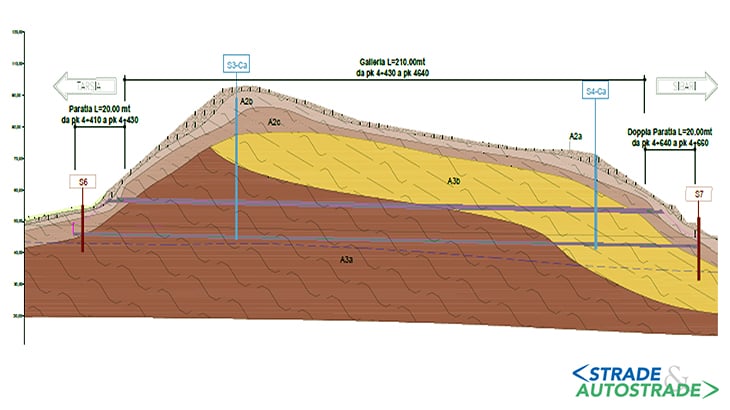
In Figura 2 sopra è mostrato il profilo geomeccanico ricostruito sulla base dei risultati (delle indagini geotecniche eseguite), nella zona interessata dalla costruzione della galleria.
In particolare, sono state riconosciute cinque unità geologiche:
- unità A2a costituita da coltre alteritica con grado di fratturazione molto elevato;
- unità A2b costituita da coltre alteritica con grado di fratturazione medio-elevato;
- unità A2c costituita da coltre alteritica con grado di fratturazione moderato;
- unità A3a costituita da litotipi scistoso-filladici;
- unità A3b costituita da litotipi a bassa scistosità/massicci.
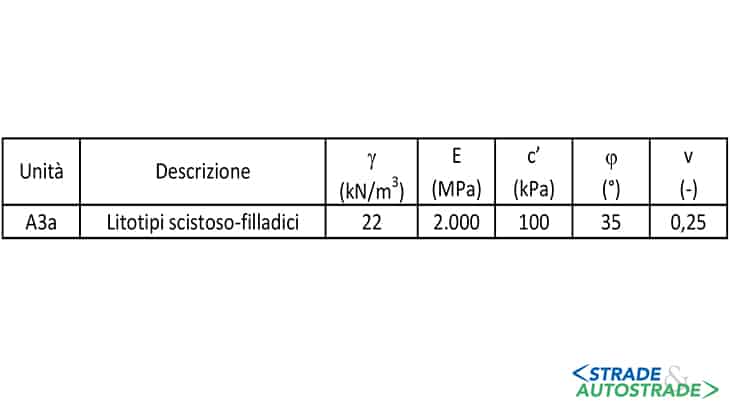
Come si può vedere dalla Figura 2, la sezione della galleria considerata ai fini della presente analisi interessa quasi completamente l’unità A3a, i cui parametri geotecnici riferiti a una Legge costitutiva elasto-plastica con criterio di rottura di Mohr-Coulomb, sono riportati nella Figura 3.
Per quanto riguarda gli aspetti idrogeologici, le misure piezometriche hanno segnalato la presenza di una falda idrica alla profondità di circa 50 m, che quindi non interagisce con i lavori di realizzazione della galleria.
La fase di diagnosi
Secondo il metodo ADECO-RS, il comportamento del fronte di scavo, al quale è legato quello della cavità, può essere sostanzialmente di tre tipi:
- fronte stabile (caso A): lo stato tenso-deformativo dell’ammasso roccioso in prossimità del fronte si mantiene essenzialmente in campo elastico;
- fronte stabile a breve termine (caso B): lo stato tensionale indotto dall’apertura del cavo raggiunge localmente la resistenza meccanica del materiale, dando luogo al verificarsi di deformazioni plastiche;
- fronte instabile (caso C): i fenomeni deformativi in campo plastico risultano rilevanti al punto da verificarsi un fenomeno di instabilità del fronte.
La definizione delle categorie di comportamento è effettuata procedendo alla valutazione di tre fattori: l’entità del processo deformativo, l’estensione della fascia di ammasso in condizioni plastiche e l’andamento della curva caratteristica, CC [2].
La fase di diagnosi è stata affrontata mediante il codice di calcolo agli elementi finiti Midas GTS NX, i cui risultati sono stati dapprima calibrati mediante il confronto con alcune soluzioni analitiche derivate da Ribacchi [3] e Vlachopoulos e Diederichs [4], che fanno riferimento a una cavità cilindrica in un mezzo indefinito con comportamento elasto-perfettamente plastico (https://www.cspfea.net/prodotti/midas-civil/caratteristiche-midas-civil/). I parametri geotecnici utilizzati nel calcolo sono quelli dell’Unità A3a, i cui valori sono elencati in Figura 3 sopra.
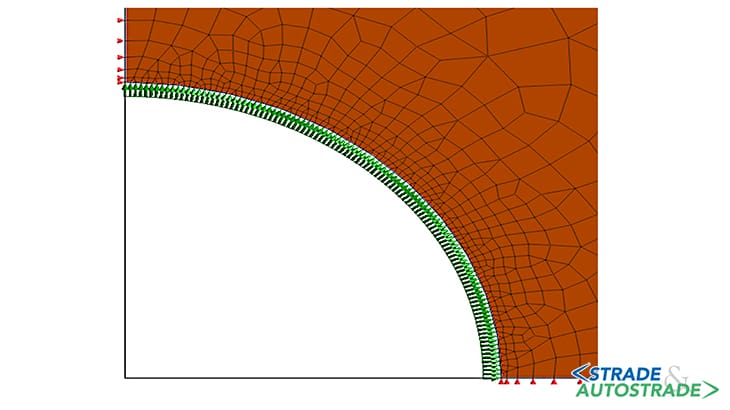
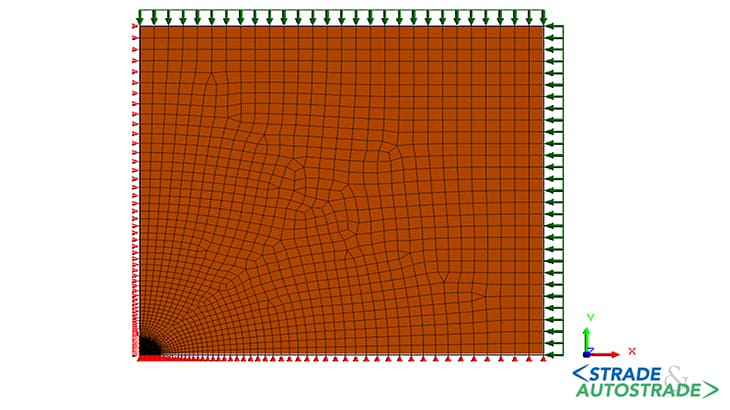
Per quanto riguarda la determinazione della curva caratteristica, l’analisi numerica è eseguita in condizioni di deformazioni piane sfruttando la simmetria del problema al fine di ridurre gli oneri computazionale. Il modello considerato ha dimensioni 140×140 m, pari a 20 volte il raggio di scavo (Figura 4 sopra).
Per ragioni di simmetria, sul lato sinistro e sul bordo inferiore del modello sono impediti gli spostamenti in direzione orizzontale e verticale, rispettivamente; sul bordo destro e alla superficie superiore è applicata una pressione pari a quella geostatica calcolata assumendo un coefficiente a riposo unitario.
È stato comunque accertato che valori ragionevolmente differenti di questo coefficiente non modificano significativamente le conclusioni dello studio. In prossimità del cavo, si è provveduto a infittire opportunamente la mesh di discretizzazione.
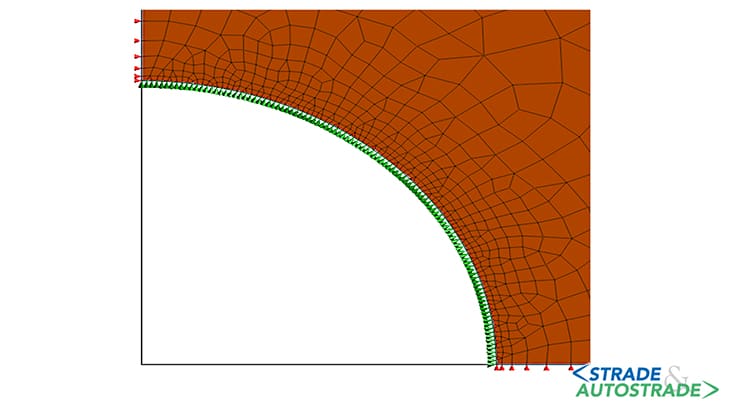
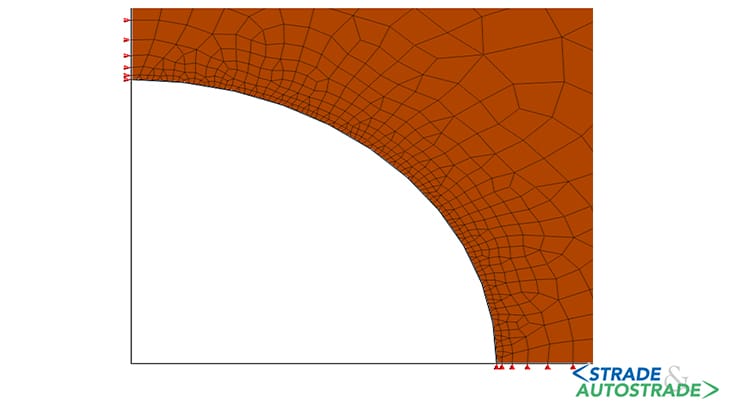
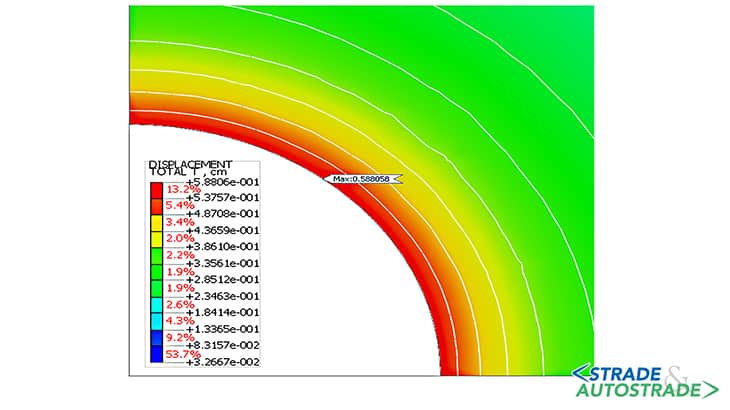
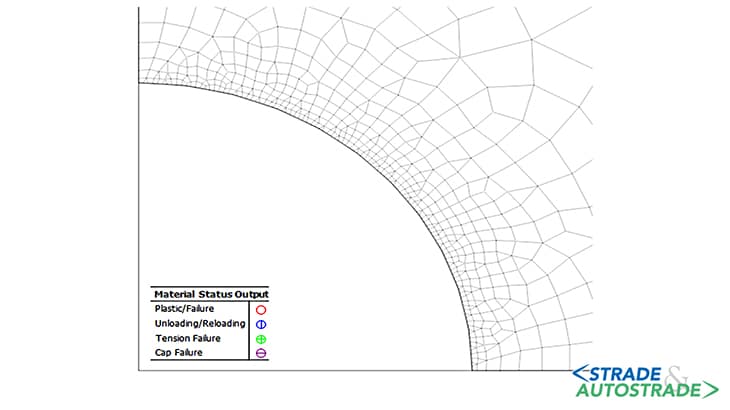
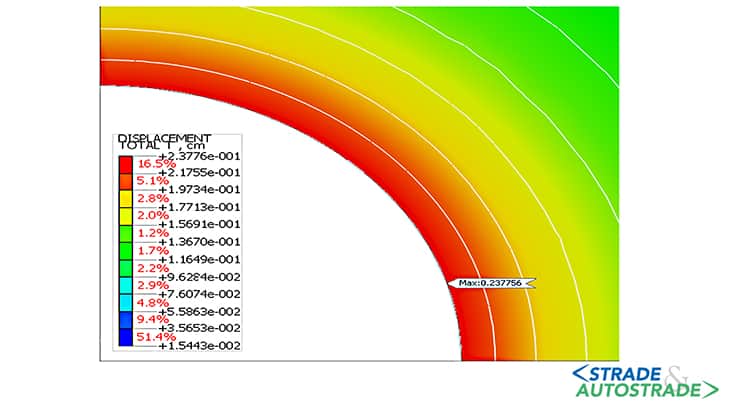
La pressione applicata sul profilo di scavo, inizialmente assunta pari allo stato di sforzo in sito P0, è progressivamente ridotta fino a zero. A titolo d’esempio, gli schemi delle Figure 5A, 5B e 5C sopra fanno riferimento alla condizione iniziale (P = 792 kPa), a un’intermedia (P = 250 kPa) e a quella finale (P = 0 kPa).
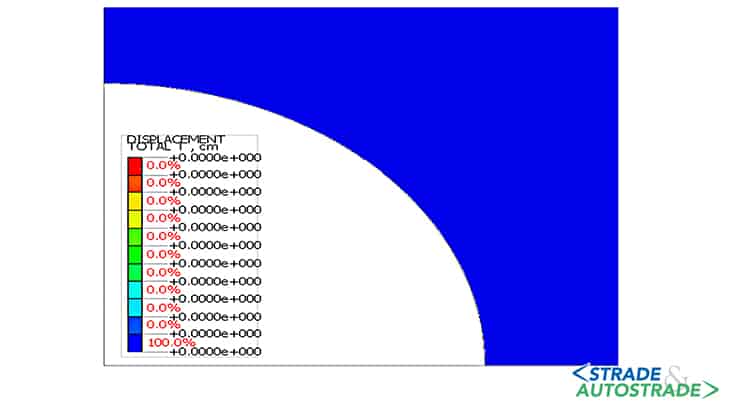
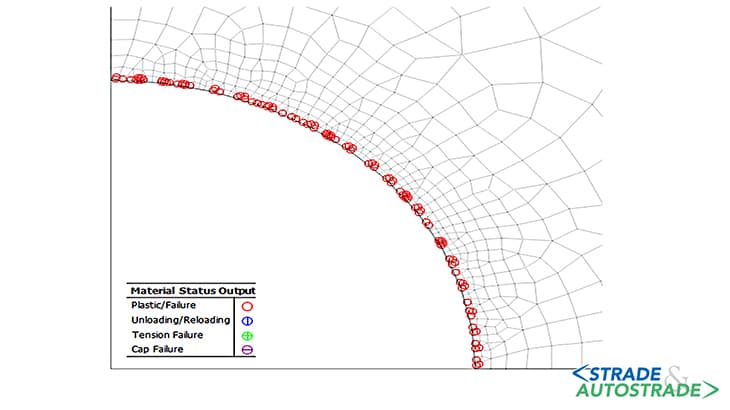
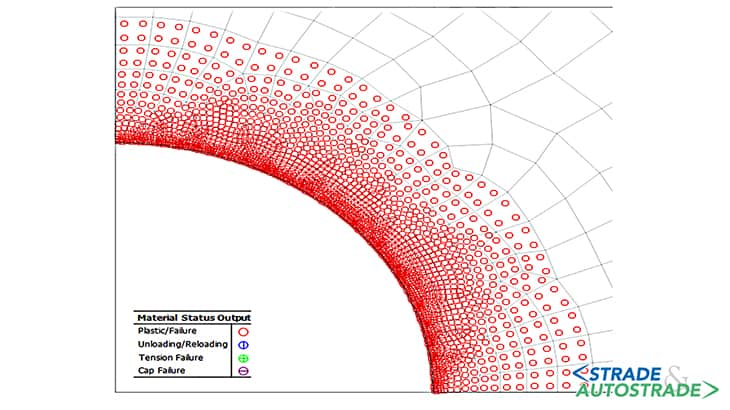
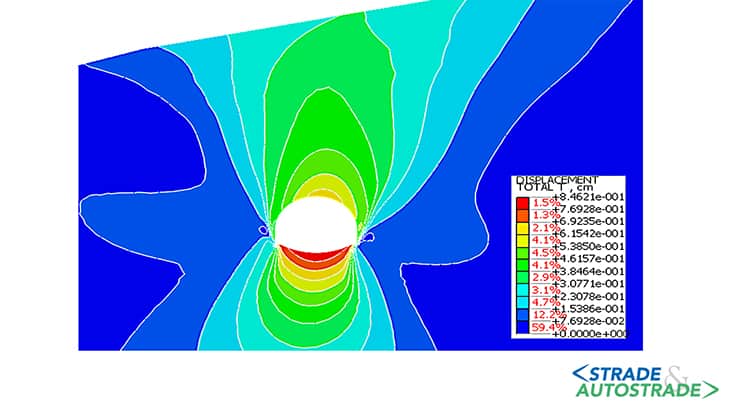
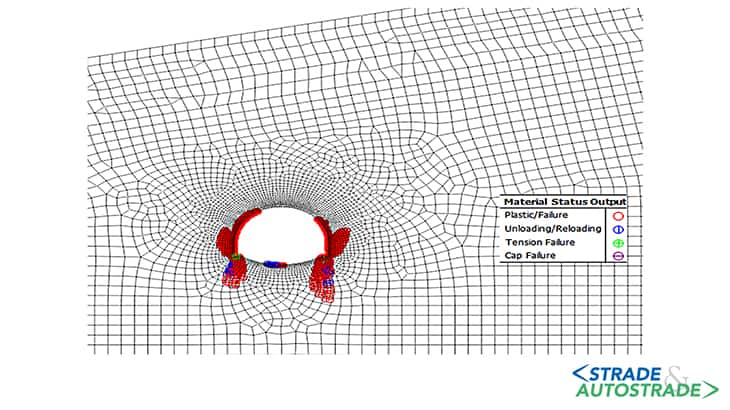
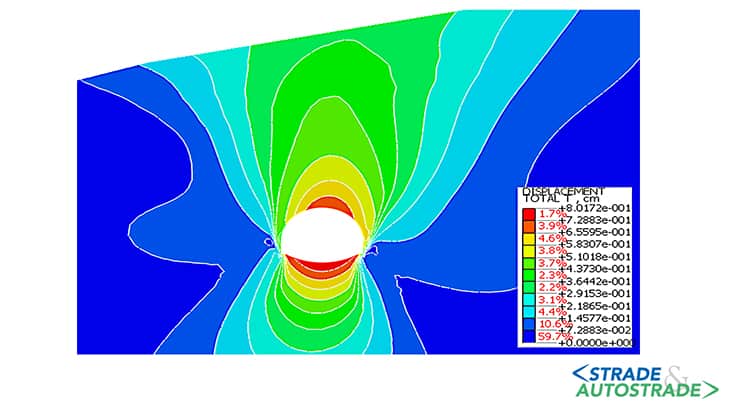
Di seguito si riportano i risultati ottenuti in termini di spostamenti massimi e di estensione della zona in condizione di plasticizzazione, per le tre condizioni considerate (Figure 6A, 6B, 6C, 6D, 6E, 6F sopra). La curva di convergenzadistanza dal fronte (LDP) è ottenuta attraverso la creazione di un modello di tipo assialsimmetrico.
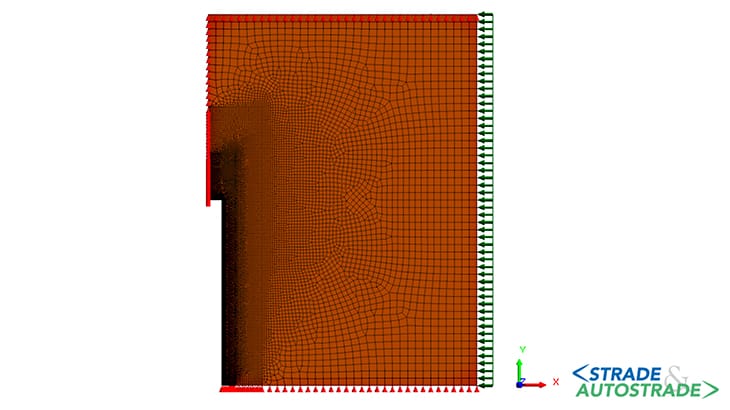
Tale modello ha un’estensione di 140 m in altezza e 200 m in lunghezza (in direzione longitudinale alla galleria), con il fronte di scavo posizionato a metà lunghezza (Figura 7).
Sui bordi orizzontali sono impediti gli spostamenti in direzione verticale, mentre sul bordo di destra è applicata una pressione pari alla tensione geostatica iniziale presente alla profondità della galleria (P0).
Il bordo verticale di sinistra rappresenta invece l’asse di simmetria del modello lungo il quale sono vincolati gli spostamenti in direzione orizzontale. Dopo aver riprodotto lo stato tensionale geostatico in condizioni di riposo, è simulato lo scavo in un’unica fase.
Il campo dello spostamento orizzontale e la posizione dei punti in condizione di plasticizzazione sono mostrati in Figura 8 sopra.
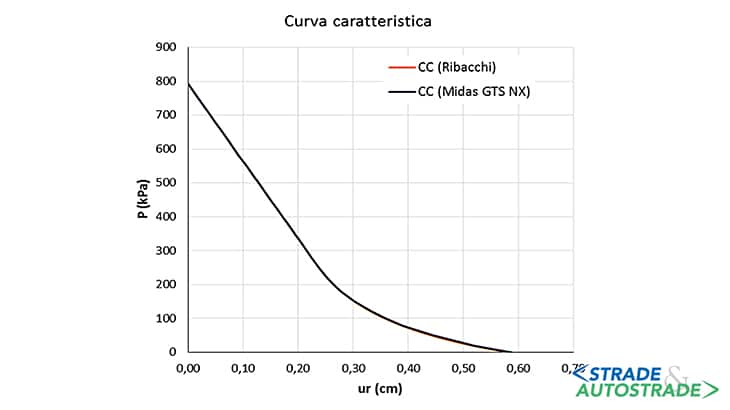
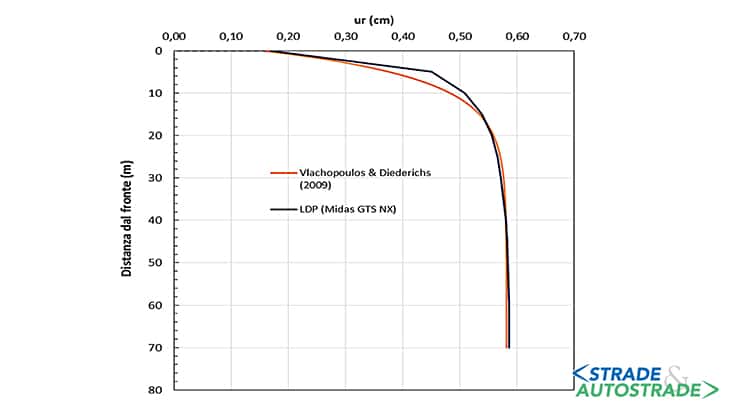
Di seguito, si riporta il confronto fra i risultati restituiti dal codice Midas e quelli ottenuti utilizzando le soluzioni analitiche di Ribacchi [3], per il calcolo della CC (Figura 9), e di Vlachopoulos e Diederichs [4] per la determinazione della LDP (Figura 10).
Dall’esame delle Figure 9 e 10, è evidente l’ottimo accordo tra simulazione numerica e soluzioni analitiche, che conferma altresì la validità del modello agli elementi finiti adottato.
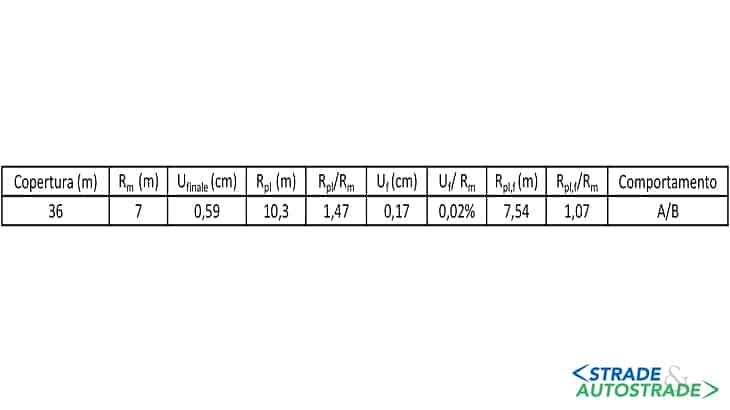
Infine, nella Figura 11 sono riportati i valori dei parametri richiesti nella fase di diagnosi, sulla base dei quali è possibile classificare il comportamento del fronte di tipo A/B, essendo caratterizzato da convergenze trascurabili, estensione limitata della fascia plastica e una curva caratteristica che presenta l’ultimo tratto con comportamento elasto-plastico.
L’analisi di stabilità del fronte di scavo
A completamento della fase di diagnosi, sono state analizzate anche le condizioni di stabilità del fronte nei riguardi di un possibile fenomeno di collasso. Per una prima valutazione del relativo coefficiente di sicurezza, FS, è stato utilizzato il metodo dell’equilibrio limite proposto da Tamez e Cornejo [5].
Assumendo i dati in input elencati in Figura 3, si ottiene un valore di FS pari a 2,67. La procedura implementata in Midas GTS NX per la determinazione di FS consiste nel ridurre progressivamente i parametri di resistenza dell’ammasso roccioso fino a causare un meccanismo di collasso del fronte di scavo (metodo SRM):
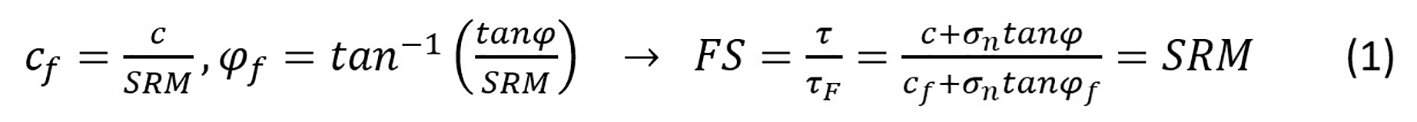
Il modello agli elementi finiti utilizzato è mostrato in Figura 12.

Come si può vedere, il modello è tri-dimensionale e considera una porzione di roccia sufficientemente estesa sia in direzione laterale e sia in profondità (al di sotto della galleria) da rendere trascurabili gli effetti delle condizioni al contorno imposte.
La mesh è realizzata mediante elementi solidi 3D, estrudendo in direzione y una geometria piana. Per prevenire il verificarsi di possibili meccanismi di collasso che non riguardano il fronte di scavo, è stata simulata la presenza di un rivestimento di prima fase tramite elementi Shell disposti in corrispondenza del tratto di galleria già scavato.
Nella Figura 13 è riportato il potenziale meccanismo di collasso restituito dalla simulazione numerica. Il valore del fattore di sicurezza è risultato pari a 2,53, valore quest’ultimo in grado di assicurare la stabilità del fronte di scavo.

La fase di terapia
Sulla base dei risultati ottenuti nella fase precedente, il comportamento del fronte è stato definito di classe A/B.
Di conseguenza, gli interventi previsti sono mirati al controllo del profilo di scavo in fase di avanzamento mediante infilaggi metallici, e al confinamento del cavo mediante la posa in opera di centine metalliche insieme ad uno strato di spritz beton fibro-rinforzato.
L’impiego dei tubi metallici si rende necessario in considerazione della limitata copertura che interessa gran parte dello sviluppo della galleria (Figura 2).
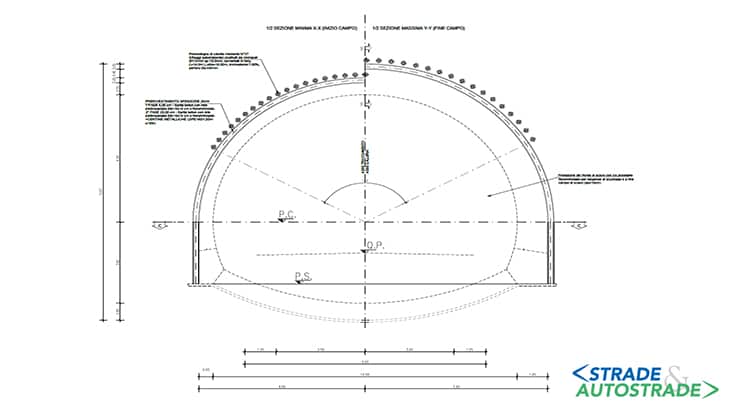
Facendo riferimento alla sezione B0 (Figura 14), gli interventi previsti sono i seguenti:
- pre-sostegno realizzato con n° 37 tubi metallici Ø114 mm e spessore = 10 mm, valvolati (2 vlv/m) e iniettati, con lunghezza L = 14 m e sovrapposizioni di 4 m;
- centine metalliche realizzate con due profilati IPE 180 poste in opera con passo di 1 m;
- spritz beton fibro-rinforzato con spessore di 25 cm, per completare il rivestimento di prima fase della galleria;
- spritz beton di regolarizzazione con spessore di 5 cm;
- spritz beton fibro-rinforzato con spessore di 10 cm, per il consolidamento del fronte di scavo;
- murette e arco rovescio in c.a. di spessore 0,80 m, gettati a una distanza dal fronte variabile in funzione del comportamento deformativo del cavo;
- rivestimento definitivo in c.a. di spessore 0,55÷1,20 m, gettato ad una distanza dal fronte variabile in funzione del comportamento deformativo del cavo;
- impermeabilizzazione con teli in PVC + TNT.
L’efficacia degli interventi previsti nel progetto è stata analizzata mediante un modello bidimensionale agli elementi finiti costruito in ambiente Midas GTS NX (Figura 15).
Siffatto modello si estende in direzione orizzontale per una distanza dall’asse della galleria pari a 20 volte il diametro del cavo e per una profondità rispetto all’asse dei centri pari a sette volte il suddetto diametro, dopo aver verificato che le condizioni al contorno non influenzano praticamente i risultati della simulazione.
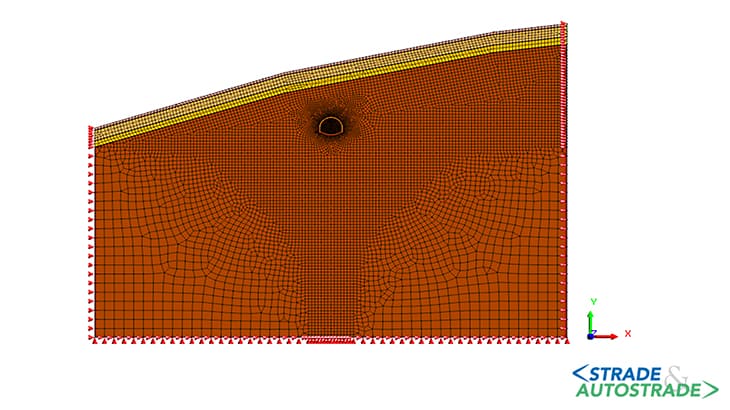
I vincoli imposti al contorno impediscono lo spostamento in direzione orizzontale sui due bordi laterali e qualsiasi spostamento al bordo inferiore del modello.
La superficie superiore riproduce il reale profilo del terreno. La mesh è costituita da 10.866 nodi e 10.792 elementi, con una maggiore concentrazione in corrispondenza del fronte di scavo.
Un particolare della sezione di scavo è mostrato in Figura 16. Il comportamento meccanico dell’ammasso roccioso è simulato mediante un modello costitutivo elasto-plastico alla Mohr-Coulomb con Legge di flusso non associata (ψ = 0) e parametri di resistenza e deformabilità indicati in Figura 3. Il coefficiente di spinta a riposo è assunto pari a 1.
Nelle elaborazioni numeriche, gli interventi di presostegno al contorno di scavo sono simulati raddoppiando le caratteristiche di resistenza e di deformabilità della fascia di terreno trattato (spessore 20 cm).

I rivestimenti, sia provvisorio che definitivo, sono modellati con elementi beam solidali al profilo di scavo. Per quanto riguarda il rivestimento provvisorio è stato considerato un modulo elastico e uno spessore equivalente (0,25 m) ottenuti omogenizzando le centine e la parete di spritz-beton; mentre, per il rivestimento definitivo, si è considerato lo spessore medio (0,85 m).
Il comportamento meccanico è pertanto descritto da una Legge elastica lineare, definita dal modulo di Young e dal coefficiente di Poisson (Figura 17). L’analisi numerica è articolata secondo stage successivi di calcolo, atti a simulare le fasi di scavo e di posa in opera degli interventi di sostegno provvisori e definitivi.
L’avanzamento progressivo del fronte di scavo è stato riprodotto attraverso il metodo delle forze fittizie di scavo (FFS). Tali forze, agenti in direzione ortogonale al profilo di scavo medesimo, avranno entità progressivamente decrescente in funzione della distanza dal fronte x, secondo una Legge di taratura definita incrociando i risultati della LDP con quelli della CC, calcolati con la procedura precedentemente descritta.
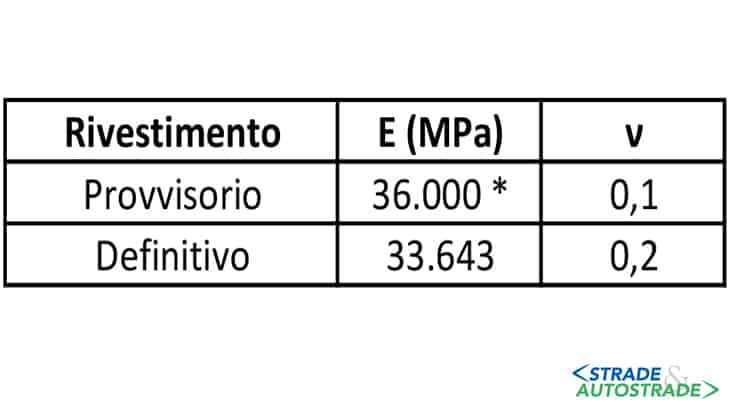
(*) valore riferito a 28 giorni di maturazione
Indicando con P0 la tensione nell’ammasso indisturbato e con Pi la tensione a una determinata distanza dal fronte, le FFS sono definite nel seguente modo:
![]()
La funzione risultante FFS-x è diagrammata in Figura 18.
Il calcolo è stato eseguito utilizzando il modulo Construction Stage implementato in Midas GTS NX.
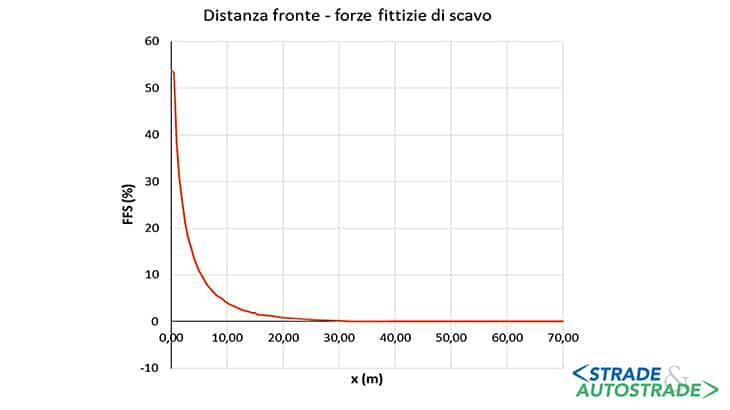
Le fasi esaminate sono le seguenti:
- definizione dello stato tensionale iniziale dell’ammasso;
- apertura del fronte di scavo, con relativa riduzione delle forze fittizie di scavo mediante la funzione LDF;
- esecuzione del primo sfondo e installazione del rivestimento provvisorio;
- esecuzione dei successivi sfondi con adeguamento delle caratteristiche meccaniche del pre-rivestimento per tener conto della maturazione dello spritz beton. A tale riguardo, si è considerato un avanzamento di 2,5 m/giorno. Tale adeguamento è reso possibile grazie al comando Change Property. In particolare, si è assunta la seguente Legge di maturazione dello spritz beton (di classe C28/35) che esprime l’aumento del modulo elastico del materiale in funzione del tempo t espresso in giorni (Figura 19):
![]()
dove:
E28 indica il modulo elastico a 28 giorni di stagionatura;
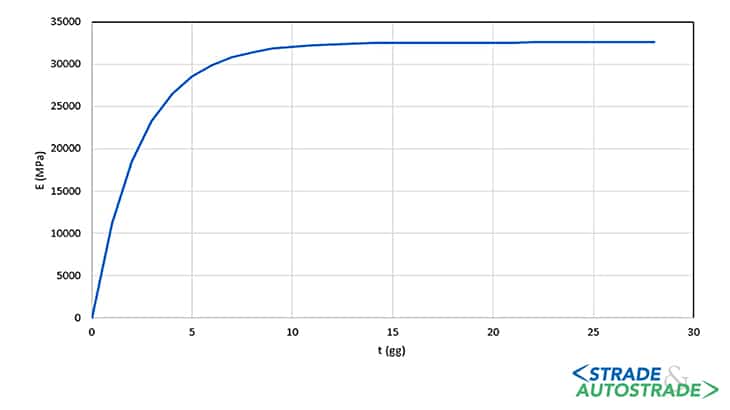
- installazione del rivestimento definitivo e completa disattivazione del rivestimento provvisorio;
- analisi del sistema in condizioni sismiche, essendo l’opera ubicata in un’area di elevata sismicità.
In quest’ultima fase, è stata eseguita un’analisi pseudo-statica impiegando i coefficienti sismici, in direzione orizzontale e verticale, forniti dalla Normativa (NTC 2018), con riferimento allo Stato Limite di salvaguardia della Vita (SLV).
Nella Figura 20 si riportano le fasi di calcolo considerate e il valore di FFS dedotto dalla curva in Figura 18. Si riportano i risultati dell’analisi in termini di spostamenti massimi e localizzazione delle zone in condizione di plasticizzazione, con riferimento alle fasi in cui si ha il massimo rilascio tensionale (fasi 4.3 e 5).

Gli spostamenti sono compresi tra 0,37 e 0,85 cm, con valori massimi in arco rovescio e in calotta. A seguito della posa in opera del rivestimento definitivo, gli spostamenti calcolati variano tra 0,43 e 0,80 cm.
Le zone plastiche si localizzano intorno al cavo interessando una fascia limitata dell’ammasso per effetto del preconsolidamento, realizzato con le centine e lo spritz beton, e dei presostegni in calotta (infilaggi metallici), con una maggiore concentrazione in corrispondenza dei piedritti e delle murette.
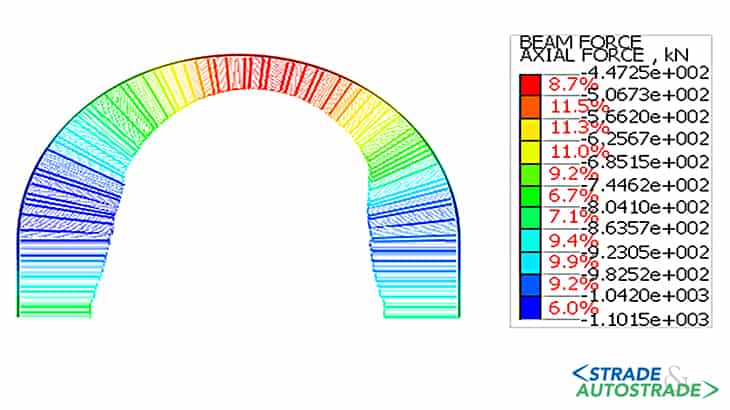
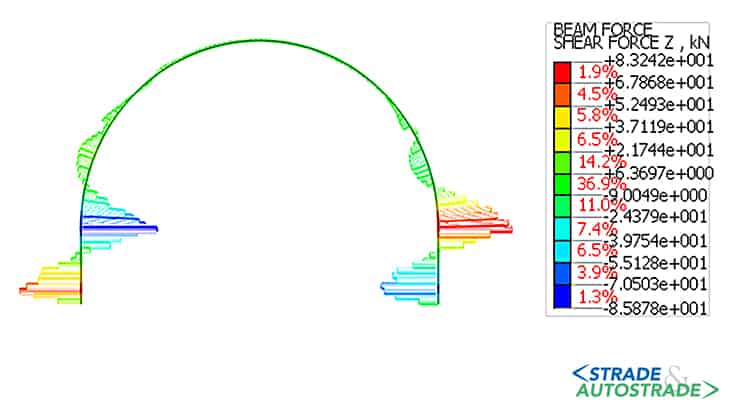
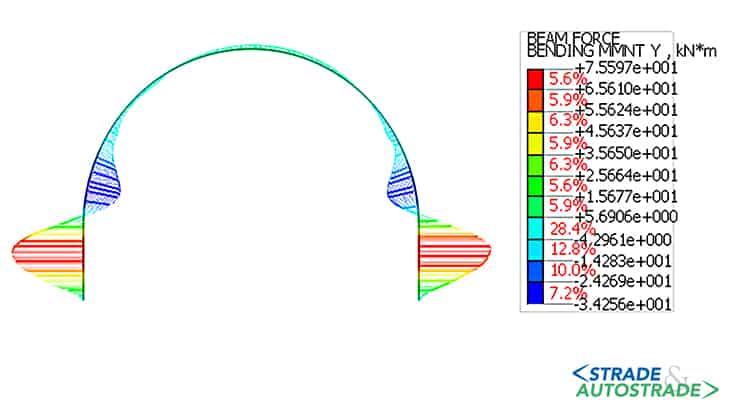
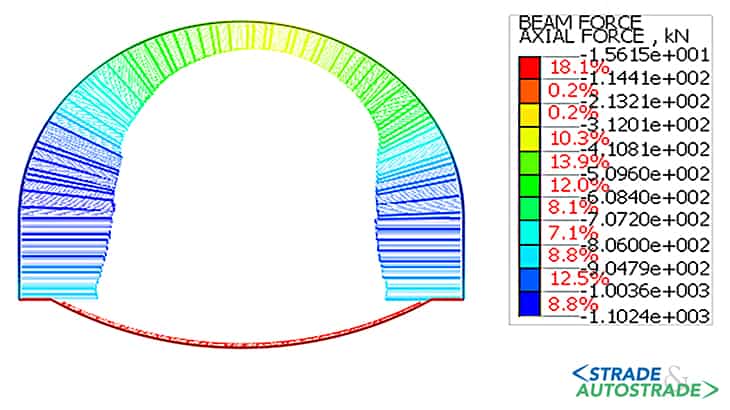
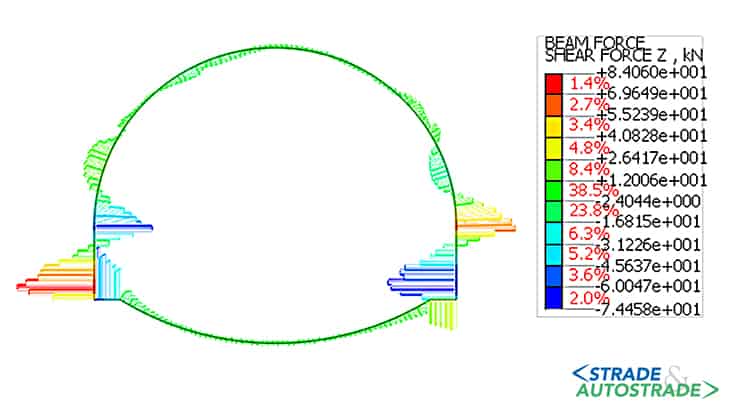
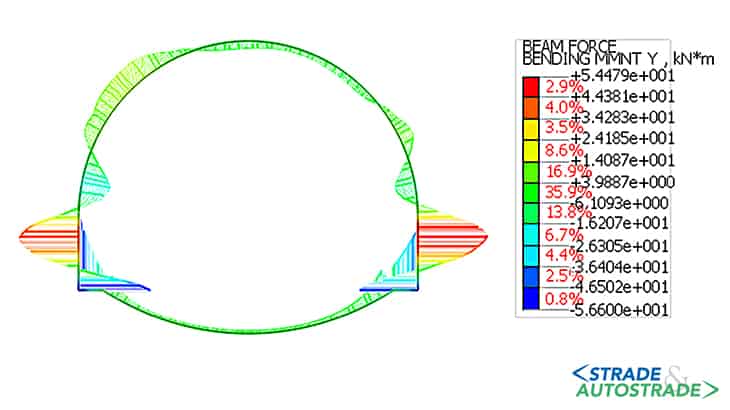
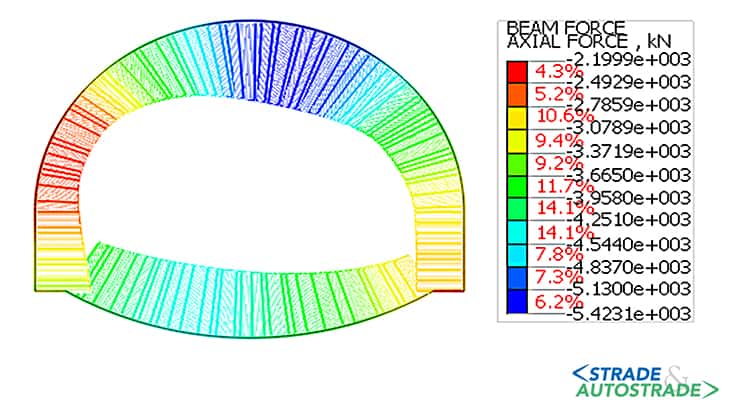
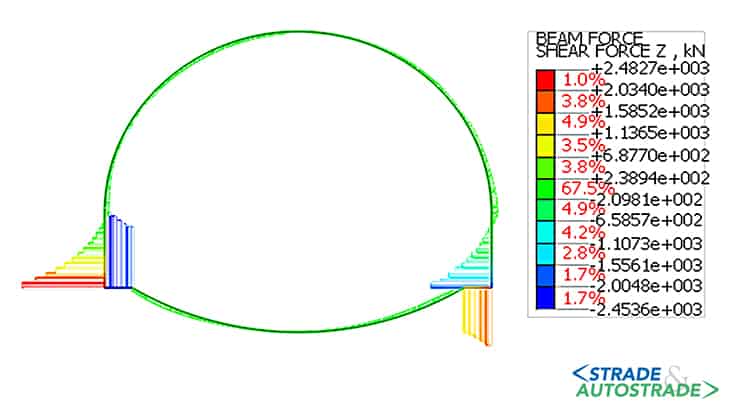
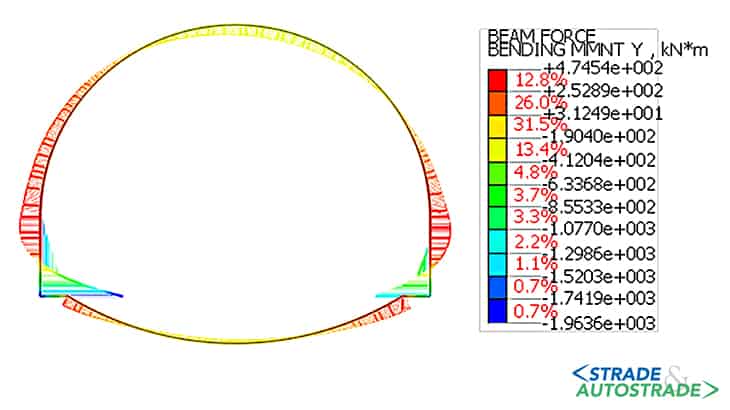
Di seguito si riportano, altresì, i diagrammi delle sollecitazioni assiali, taglianti e flettenti nel rivestimento provvisorio (fase 4.3) e in quello definitivo (fasi 5 e 6).
L’andamento delle sollecitazioni risulta dissimmetrico dal momento che la galleria è parietale. Le sollecitazioni nel rivestimento, sia provvisorio che definitivo, indicano uno stato di sollecitazione prevalentemente di compressione, che varia significativamente in condizioni sismiche allorché si registra un notevole incremento del momento flettente.
I valori del momento flettente e del taglio risultano ridotti in calotta e in arco rovescio, mentre sono maggiori nei piedritti e nelle murette. Allo stato attuale (Novembre 2022), la galleria è in fase di costruzione.
Nelle Figure 24 e 25 sotto sono documentati i lavori relativi all’installazione degli infilaggi e alla realizzazione dello scavo per la posa in opera del rivestimento di prima fase. Inoltre, le immagini confermano le previsioni progettuali circa il comportamento del fronte di scavo nella sezione considerata.
Conclusioni
Nel presente articolo, sono state descritte le principali fasi del progetto di una galleria in scavo tradizionale in fase di realizzazione, in provincia di Cosenza. La progettazione è stata condotta secondo il metodo ADECO-RS.
La previsione del comportamento tenso-deformativo dell’ammasso roccioso a seguito dello scavo è stata effettuata mediante modelli agli elementi finiti in ambiente Midas GTS NX, calibrati attraverso il confronto con i risultati ottenuti utilizzando alcune soluzioni analitiche disponibili in letteratura.
Il codice Midas GTS NX è stato altresì impiegato per il dimensionamento degli interventi di consolidamento, sia provvisori e sia definitivi. Midas GTS NX è stato fornito da CSPFea, rivenditore ufficiale italiano del software Midas.
Dati tecnici
- Stazione Appaltante: Provincia di Cosenza
- Contraente Generale e Impresa esecutrice: Franco Giuseppe Srl
- Project Manager e Direzione di Cantiere: Ing. Antonio Salvatore Trifoli
- Progetto preliminare e definitivo: Settore Viabilità e Manutenzione del Territorio della Provincia di Cosenza
- Progetto esecutivo: Ing. Pietro Lappano della HYpro Srl
- Collaudo: Ing. Stefano Aiello e Ing. Antonio Nisticò
- RUP: Ing. Michele Arcuri
- Direzione dei Lavori: Ing. Vincenzo Secreti
- Direttore operativo: Ing. Beniamino Bria
- Responsabile Sicurezza: Ing. Pietro Lappano
- Esecutori dei Lavori: Franco Giuseppe Srl
- Subappaltatori: FE.VI Srl, Emanuele Milena, Cilar Srls, Bicamis Srl e Soil Pali
- Importo dei lavori: 9.848.509,43 Euro
- Durata dei lavori: 440 giorni
- Data di consegna: 14 Maggio 2021
- Data di ultimazione: 28 Febbraio 2023
Bibliografia
[1]. P. Lunardi – “Progetto e costruzione di gallerie secondo l’approccio basato sull’analisi delle deformazioni controllate nelle rocce e nei suoli”, “Quarry and construction”, Marzo 1994, Marzo 1995, Aprile 1996.
[2]. W.A. Amberg, G. Lombardi – “Une méthode de calcul élasto-plastique de l’état de tension et de déformation autour d’une cavité souterraine, 2eme partie”, Proc. 3rd Cong. Int. Soc. Rock Mechanics, Vol. IIB, Denver, 1974.
[3]. R. Ribacchi, R. Riccioni – “Stato di sforzo e di deformazione intorno ad una galleria circolare”, Gallerie e Grandi Opere Sotterranee, 1977.
[4]. N. Vlachopoulos, M.S. Diederichs – “Improved Longitudinal displacement profiles for convergence confinement analysis of deep tunnel”, Rock mechanics and rock engineering, Vol. 42, n. 2, pp. 131-146, 2009.
[5]. E. Tamez, V. Cornejo – “Instability at the face: its repercussion for tunnelling technology”, Tunnels & Tunnelling, April 1989.
[6]. O. Aydan, M. Sezaki, T. Kawata, G. Swoboda, A. Moussa – “Numerical modelling for the representation of shotcrete hardening and face advance of tunnels excavated by bench excavation method”, Numerical models in geomechanics, Pande & Pietruszczak (eds.), Taylor & Francis, London, pp. 707-716, 1992.
> Se questo articolo ti è piaciuto, iscriviti alla Newsletter mensile al link http://eepurl.com/dpKhwL <