Un’analisi probabilistica per la stabilità di scarpate secondo RLEM – seconda parte ![]() For English version: https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-2/
For English version: https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-2/
La prima parte dell’articolo, proposta su “S&A” n° 141 Maggio/Giugno 2020, è online su https://www.stradeeautostrade.it/ambiente-e-territorio/unanalisi-probabilistica-per-la-stabilita-di-scarpate-secondo-rlem-prima-parte/.
La stabilità della scarpata 1D e quasi-stocastica
L’uso dell’analisi spazialmente variabile influenza la probabilità calcolata per l’instabilità delle scarpate.
[1] affermano che per i modelli di scarpate con un fattore medio di sicurezza maggiore di 1, tenendo conto della variabilità spaziale delle proprietà dei materiali (ad esempio, coesione e densità) si ottiene una minore probabilità di instabilità, rispetto alla stessa analisi senza utilizzare la variabilità spaziale.
Un’analisi probabilistica che non considera la variabilità spaziale ha dimostrato di provocare probabilità di instabilità non realistiche e eccessivamente conservative [1].
La generazione convenzionale di campo casuale 1D nei problemi di stabilità del pendio si riferisce alla analisi di parametri stocastici del suolo lungo una superficie di scorrimento predeterminata e plausibile passante attraverso il dominio del suolo.
Non si ritiene che ciò produca risultati realistici in quanto le proprietà del suolo sono considerate esclusivamente lungo una superficie di cedimento prescritta che viene normalmente raggiunta da alcune analisi deterministiche che adottano mediamente i parametri del terreno.
Molto recentemente [2] sono stati confrontati i risultati di tali analisi stocastiche 1D con alcune soluzioni analitiche probabilistiche tradizionali per la geometria del pendio qui studiate.
In precedenza, [1] hanno confrontato i risultati di alcune analisi di stabilità del pendio stocastiche 2D con la descrizione del campo casuale 1D dei parametri del suolo, come spiegato sopra. In [3] sono anche state effettuate analisi stocastiche 1D simili sulla stabilità di tagli verticali.
Una soluzione probabilmente più praticabile può essere fornita se invece della semplice modellizzazione stocastica 1D, venisse adottata una descrizione del campo casuale quasi stocastica.
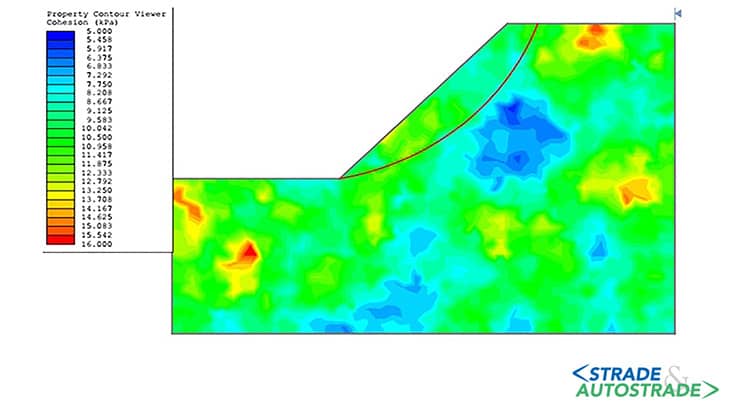
Ciò implica che i parametri del suolo spazialmente variabili vengono prima analizzati in tutto il dominio 2D.
Successivamente, i valori corrispondenti attraverso la superficie di scorrimento prestabilita vengono raccolti e introdotti nei calcoli basati sulla porzione (concio) del pendio per ciascuna simulazione MC.
La Figura 1 mostra un’analisi di stabilità del pendio quasi-stocastica e la superficie di scorrimento presunta. Vale la pena ricordare che la superficie di scorrimento prescritta può by-passare i punti più deboli in alcune simulazioni MC come appare nella Figura 1.
Questo comportamento di elusione, inerente ai calcoli di stabilità del pendio quasi stocastico, è davvero inevitabile; tuttavia, se confrontato con l’approccio 1D semplice e certamente non realistico, si ritiene che questa analisi sia più performante.
Di seguito, verranno fornite e discusse alcune illustrazioni comparative della distribuzione del fattore di sicurezza.
Come accennato in precedenza, l’ottimizzazione di Surface Altering è stata utilizzata in questo studio insieme al metodo di ricerca Cuckoo per trovare il fattore critico di sicurezza per ogni calcolo.
Risultati e discussioni
I risultati delle simulazioni MC per diversi approcci stocastici sono stati forniti nelle forme di Probability Distribution Function (PDF) e Cumulative Distribution Function (CDF).
Diverse formulazioni di stabilità della pendenza basate sulla fetta (concio), in particolare il metodo Janbu semplificato, il metodo Spencer e il metodo Morgenstern-Price sono state scelte a scopo dimostrativo, mentre i risultati del metodo Bishop semplificato sono stati ignorati per il motivo spiegato in precedenza.
Sono state presentate le analisi di stabilità stocastica circolare e non circolare insieme allo schema quasi stocastico. Quest’ultimo è considerato un’alternativa all’analisi della stabilità della scarpata stocastica 1D.
In generale, si osserva che l’approccio di stabilità del pendio RLEM stocastico non circolare produce valutazioni di stabilità del pendio più conservative.
Come previsto nelle scarpate eterogenee, l’approccio non circolare basato su LEM è più adatto a catturare la superficie di rottura che passa attraverso il percorso più debole.
Si osserva inoltre che le analisi di stabilità del pendio RLEM quasi stocastiche hanno reso le previsioni del fattore di sicurezza mediamente meno conservative.
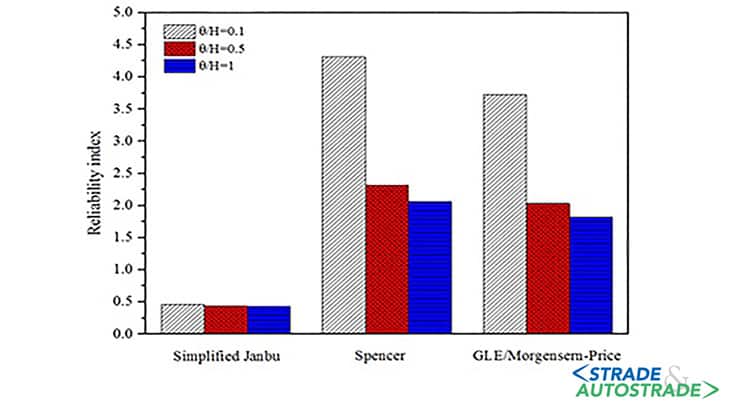
L’analisi quasi stocastica presentata in Figura 2 ha comportamento giustificabile in quanto alcuni punti deboli sono inclini ad essere aggirati quando si considera una superficie di scorrimento prestabilita nell’approccio quasi stocastico.
Nel complesso, la superiorità dell’approccio di stabilità del pendio RLEM non circolare rispetto agli approcci circolari è confermata confrontando i fattori di sicurezza medi con approcci diversi.
Si osserva inoltre che il cosiddetto approccio quasi-stocastico, pur fornendo risultati non conservativi di analisi della stabilità della pendenza, potrebbe essere considerato un’alternativa coerente al controverso approccio stocastico 1D.
Da un’altra osservazione dai risultati dell’analisi di stabilità della pendenza si evince che trascurare l’auto-correlazione dei parametri di resistenza nell’approccio RLEM non circolare renderebbe risultati non conservativi come illustrato dai grafici di affidabilità per differenti scale di fluttuazione (Figura 2).
L’indice di affidabilità è stato acquisito dalla linearizzazione della funzione di prestazione attorno al valore medio del fattore di sicurezza che rappresenta una variabile casuale nell’approccio FOSM.
La funzione di prestazione è stata adottata come M = FS – 1 e l’indice di affidabilità è stato stimato attraverso β = (μ (FS) – 1) / (σ FS)).
Il confronto verticale delle curve CDF per diverse scale di fluttuazione può anche portare a conclusioni sull’impatto della scala di fluttuazione e sull’indice di affidabilità delle analisi di stabilità del pendio.
Sebbene le differenze tra i fattori di sicurezza medi corrispondenti alle diverse scale di fluttuazione non siano del tutto distinguibili, le curve CDF più piatte nella scala più ampia di fluttuazione supportano la tesi secondo cui l’aumento della scala di fluttuazione determina una riduzione dell’affidabilità.
Al limite, quando si incontra una grande lunghezza di correlazione, i risultati circolari e quasi-stocastici quasi coincidono. In tali circostanze, le analisi di stabilità delle scarpate sono effettivamente un insieme di casi casuali omogenei che convergono in media alla soluzione deterministica.
I risultati in tale condizione dovrebbero essere comparabili con le risposte probabilistiche [2]. Le curve CDF sono buone per mostrare la coerenza in questi casi specifici.
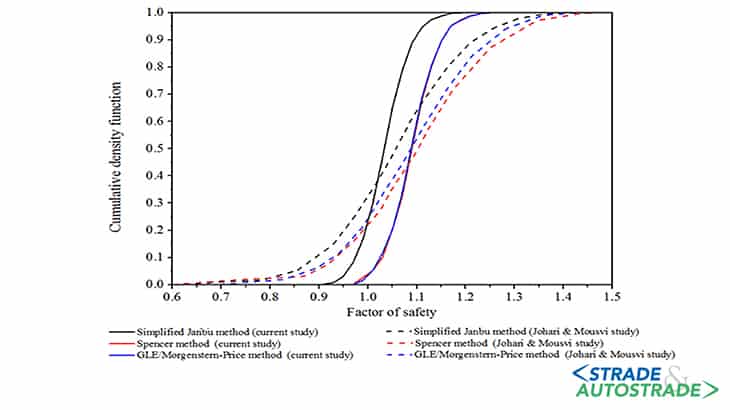
Tuttavia, come illustrato nella Figura 3, i risultati delle analisi circolari stocastiche complete RLEM per l’ampia scala di fluttuazione non sono in stretta conformità con i risultati delle analisi probabilistiche [2].
Sebbene i risultati siano in buon accordo in termini di valori medi, sembra che la variabilità dei dati del fattore di sicurezza non sia della stessa origine. La discrepanza può essere attribuita alla differenza nella funzione di distribuzione della probabilità tra i due studi.
Inoltre, è stato dimostrato che trascurare la correlazione incrociata tra i parametri di resistenza nei problemi di stabilità del pendio può dare origine a risultati conservativi.
Ciò può essere supportato dai grafici dell’indice di affidabilità, dei casi corrispondenti a parametri di resistenza indipendenti e con correlazione incrociata per l’approccio stocastico non circolare.
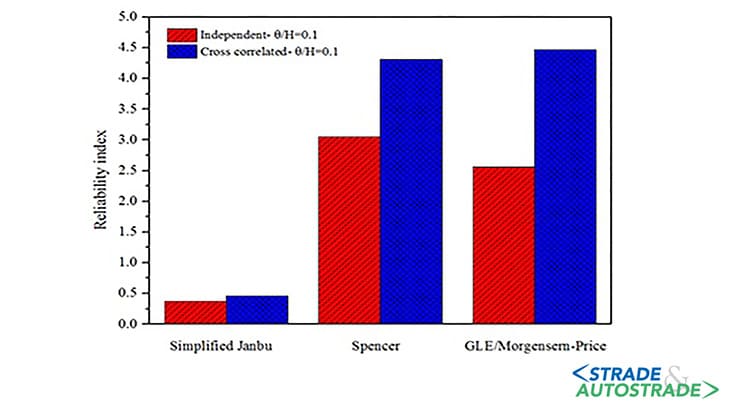
La Figura 4 indica chiaramente che trascurare la correlazione incrociata negativa tra la coesione e l’angolo di attrito del terreno, a causa della maggiore possibilità di formazione di punti deboli, porterà ad un aumento del potenziale di instabilità del pendio.
Poiché i parametri di resistenza sono presi negativamente correlati, quando la coesione in alcuni elementi diventa bassa, il motore di generazione del campo dell’angolo di attrito renderà presumibilmente valori elevati per soddisfare i requisiti di correlazione incrociata.
Pertanto, considerando la correlazione incrociata tra i parametri di resistenza dovrebbe indurre una riduzione della probabilità di instabilità della scarpata eterogenea, come appare dalla Figura 4.
Conclusioni
Le seguenti conclusioni derivano dal confronto di risultati tra diversi approcci RLEM, ovvero gli approcci RLEM stocastici completi circolari e non circolari e i modelli di ricerca di blocchi RLEM quasi stocastici.
La superficie di scorrimento non circolare, a causa della sua versatilità nel catturare geometrie di instabilità arbitrarie, si è dimostrata più efficiente nel rilevare le condizioni di stabilità più critiche rispetto ai tradizionali algoritmi circolari basati sulle “slice” (conci).
È stato dimostrato che l’analisi non circolare produrrà fattori di sicurezza mediamente inferiori per le pendenze eterogenee. Nel complesso, è stato indicato che l’indice di affidabilità delle scarpate non omogenee, considerando la geometria di instabilità non circolare, riduce l’indice di affidabilità della pendenza producendo una maggiore probabilità di instabilità.
È stato dimostrato che le analisi RLEM quasi stocastiche rendono le valutazioni di stabilità non conservative restituendo un fattore di sicurezza medio più elevato rispetto agli approcci RLEM stocastici completi circolari/non circolari. Tuttavia, si sostiene che può ancora essere un’alternativa fattibile all’approccio impreciso della stabilità del pendio 1D.
La struttura di auto-correlazione dei parametri di resistenza ha dimostrato di avere un serio impatto sull’affidabilità delle analisi di stabilità dei pendii attraverso l’adozione degli approcci RLEM.
Ignorare la struttura di correlazione dei parametri di resistenza, vale a dire la coesione e l’angolo di attrito del terreno, porterà a un aumento degli indici di affidabilità e quindi alla valutazione di stabilità non conservativa. La correlazione incrociata negativa tra i parametri di resistenza ha dimostrato di avere un’influenza importante sulle previsioni del fattore di sicurezza.
È stato indicato che trascurare la struttura della covarianza dei molteplici parametri di resistenza coinvolti nell’analisi di stabilità di pendenze eterogenee restituirà analisi di stabilità conservative nella prospettiva di progettazione basata sull’affidabilità.
Bibliografia
[1]. S. Javankhoshdel, B. Cami, R.J. Bathurst, T. Yacoub, B. Corkum – “Probabilistic analysis of cohesive-frictional slopes using the RLEM (circular and con-circular) and the RFEM”, in Proceedings of 70th Canadian Geotechnical Conference, Ottawa, Canada, September 2017.
[2]. A. Johari, S. Mousavi – “An analytical probabilistic analysis of slopes based on limit equilibrium methods”, Bulletin of Engineering Geology and the Environment, 1-15, 2018.
[3]. J.R. Chenari, M. Zamanzadeh – “Uncertainty assessment of critical excavation depth of vertical unsupported cuts in undrained clay using random field theorem. Scientia Iranica. Transaction A, Civil Engineering, 23(3), 864, 2016.
La prima parte dell’articolo è online su https://www.stradeeautostrade.it/ambiente-e-territorio/unanalisi-probabilistica-per-la-stabilita-di-scarpate-secondo-rlem-prima-parte/.
![]() For English version: https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-2/
For English version: https://www.stradeeautostrade.it/en/environment-prevention-conservation/full-and-quasistochastic-slope-stability-analysis-using-random-limit-equilibrium-method-rlem-part-2/
> Se questo articolo ti è piaciuto, iscriviti alla Newsletter mensile al link http://eepurl.com/dpKhwL <

