Questo studio propone un algoritmo di ricerca basato su una tecnica Swarm (Particle Swarm Optimization – PSO) che consente di ottimizzare la geometria dei tracciati stradali, minimizzando una funzione di costo che tiene conto di voci condizionanti la geometria del tracciato e di penalità relative ai vincoli presenti nel territorio.
Definire un tracciato corretto, nel rispetto dei vincoli, può richiedere molto tempo e solo l’esperienza del Progettista e una approfondita analisi del territorio e dei relativi vincoli consentono di definire una soluzione idonea, tra le infinite possibili. Recentemente numerosi Studiosi hanno cercato di automatizzare questa procedura per supportare i Tecnici nella progettazione, consentendo un celere confronto delle diverse soluzioni ed evidenziando i percorsi migliori.
La Swarm Intelligence ed il metodo PSO
La Swarm Intelligence è una tecnica introdotta da Kennedy ed Eberhart basata sulle caratteristiche sociali di interazione riscontrate in sciami di insetti o stormi di uccelli. In questi sistemi, senza un vero leader, si riscontrano comportamenti globali molto complessi che permettono di raggiungere obiettivi comuni degni di nota.
L’algoritmo PSO deriva dallo studio del comportamento degli stormi di uccelli nella ricerca del cibo: si suppone che ogni uccello non conosca l’effettiva posizione del cibo ma solo la sua distanza da esso e che modifichi istante per istante la sua velocità (quindi la sua posizione) per minimizzare tale distanza.
L’ottimizzazione avviene in funzione dell’esperienza passata (miglior posizione raggiunta) della particella e del gruppo. Bilanciando opportunamente i vari contributi si può garantire una completa esplorazione dello spazio di ricerca e il superamento di ottimi locali.
Ciascuna soluzione viene valutata attraverso una funzione di costo da minimizzare, per permettere un confronto opportuno e credibile delle diverse alternative e modificare le soluzioni nel modo più opportuno.
La modellazione del problema
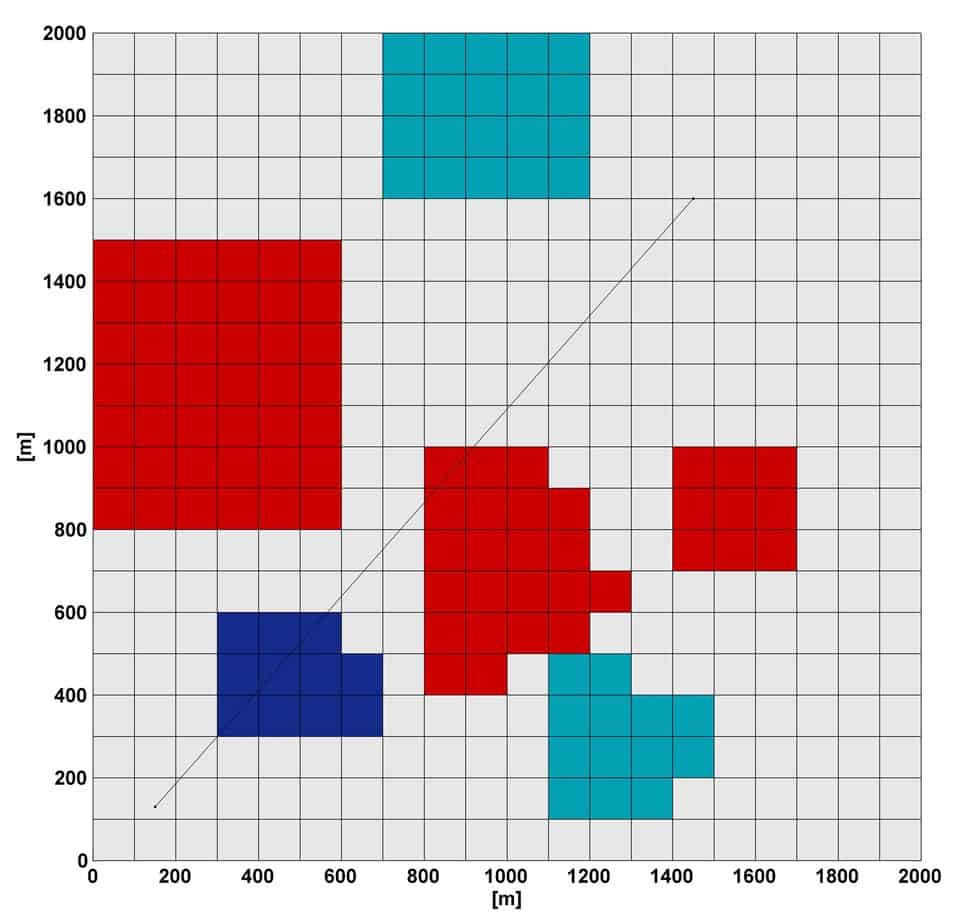
La soluzione cercata è costituita dalla definizione di un tracciato che unisca due punti noti, minimizzando i costi totali e garantendo il soddisfacimento di vincoli operativi e di progetto. L’area di studio è opportunamente ricreata attraverso specifiche griglie, contenenti informazioni relative alla tipologia dei vincoli presenti nel territorio e al loro livello di criticità.
La singola soluzione si prodotta dall'algoritmo è costituita dalle coordinate dei vertici interni della poligonale d’asse. Per ogni soluzione, vengono ottimizzati i raggi delle curve circolari, scelti con un apposito algoritmo all’interno di un intervallo definito nel rispetto delle prescrizioni normative, tenendo conto delle condizioni di continuità. La funzione di costo è stata impostata tenendo conto delle seguenti componenti:
- costi dipendenti dalla lunghezza, Clun: sovrastruttura e sua manutenzione, eventuali elementi di corredo o di sicurezza, spese di impatto ambientale, ecc.;
- costi dipendenti dalla posizione, Cpos: aliquote di spesa direttamente collegate alle aree attraversate dal tracciato, quali le spese di esproprio e di stabilizzazione e sistemazione del piano di posa;
- costi per gli utenti, CU: utilizzo dei veicoli, tempi di percorrenza e costo sociale legato agli incidenti stradali.
Per permettere una rapida convergenza del modello sono stati introdotti dei particolari operatori che modificano le soluzioni ottenute dopo ogni ciclo, garantendo una maggiore esplorazione dello spazio di ricerca: sono stati considerati un operatore di straight mutation (modifica le coordinate di un dato vertice per sostituire alla curva corrispondente un rettifilo) e uno di random mutation (modifica la coordinata di un vertice della poligonale con un valore casuale all’interno dell’area di studio). Nella procedura sono state utilizzate delle penalità, che introducono un incremento del costo della soluzione proporzionale all’entità della trasgressione, per allontanare lo sciame di particelle da soluzioni inaccettabili e scorrette. Per quanto riguarda le funzioni di penalità geometriche, sono stati considerati i seguenti aspetti, ispirati dalle Norme Italiane:
- penalità legata al raggio minimo, PRmin;
- penalità legata al rapporto tra i raggi, PR;
- penalità legata alla lunghezza del rettifilo minimo, Pret.
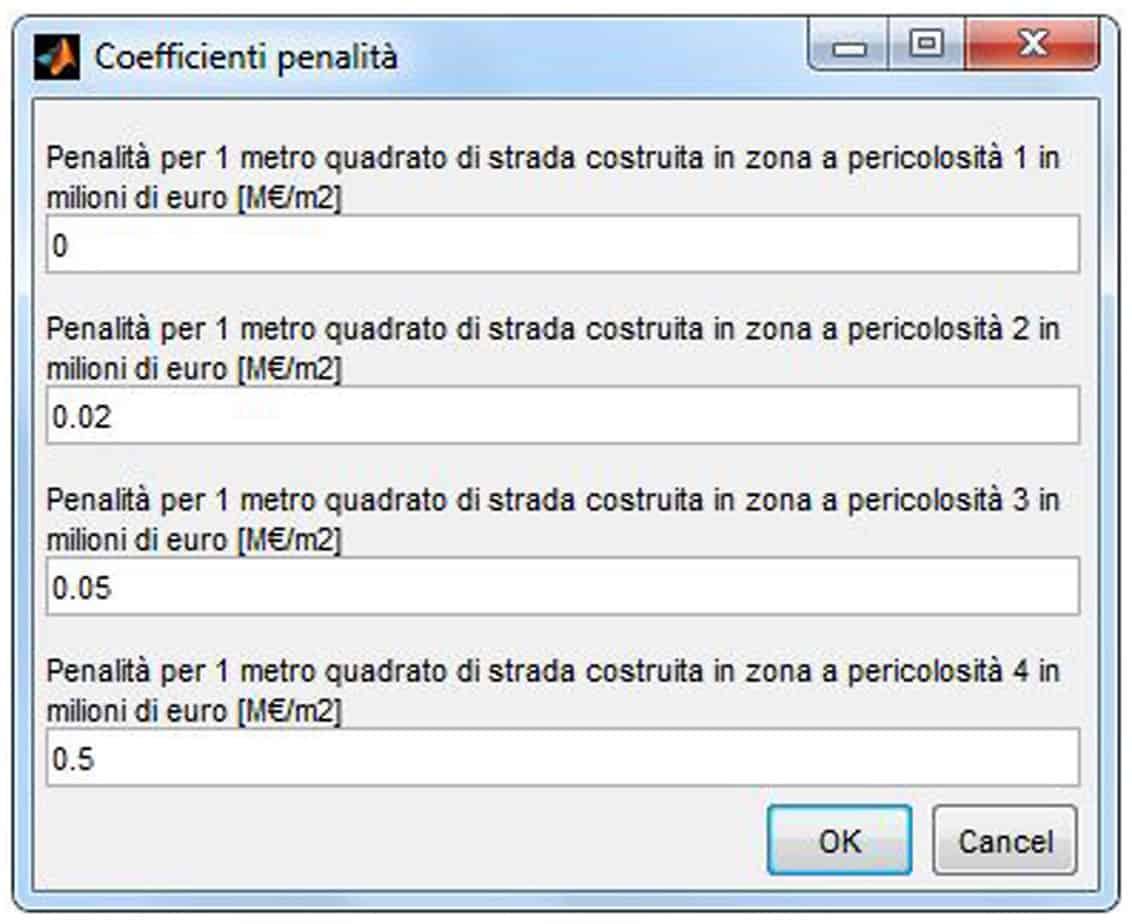
Per le funzioni di penalità legate ai vincoli ambientali, è opportuno richiamare la nota definizione del rischio (R = PVE), secondo cui il rischio è pari al prodotto dell’Esposizione, per la Vulnerabilità dell'opera, per la Pericolosità dell’area. Considerando E costante (infrastruttura e utenti), per mantenere costante R è necessario sostenere forti costi per abbattere V, al crescere di P. Nel dettaglio, per il calcolo si è fatto riferimento ad una apposita mappa, indicativa della pericolosità ambientale globale, associando alle diverse celle rappresentative dell’area di studio valori di pericolosità variabili e contraddistinti da livelli di costo crescenti. Il valore globale di penalità è ottenuto semplicemente moltiplicando la lunghezza dei tratti di strada ricadenti nelle singole celle per il relativo costo unitario.
Esempi numerici e discussione dei risultati
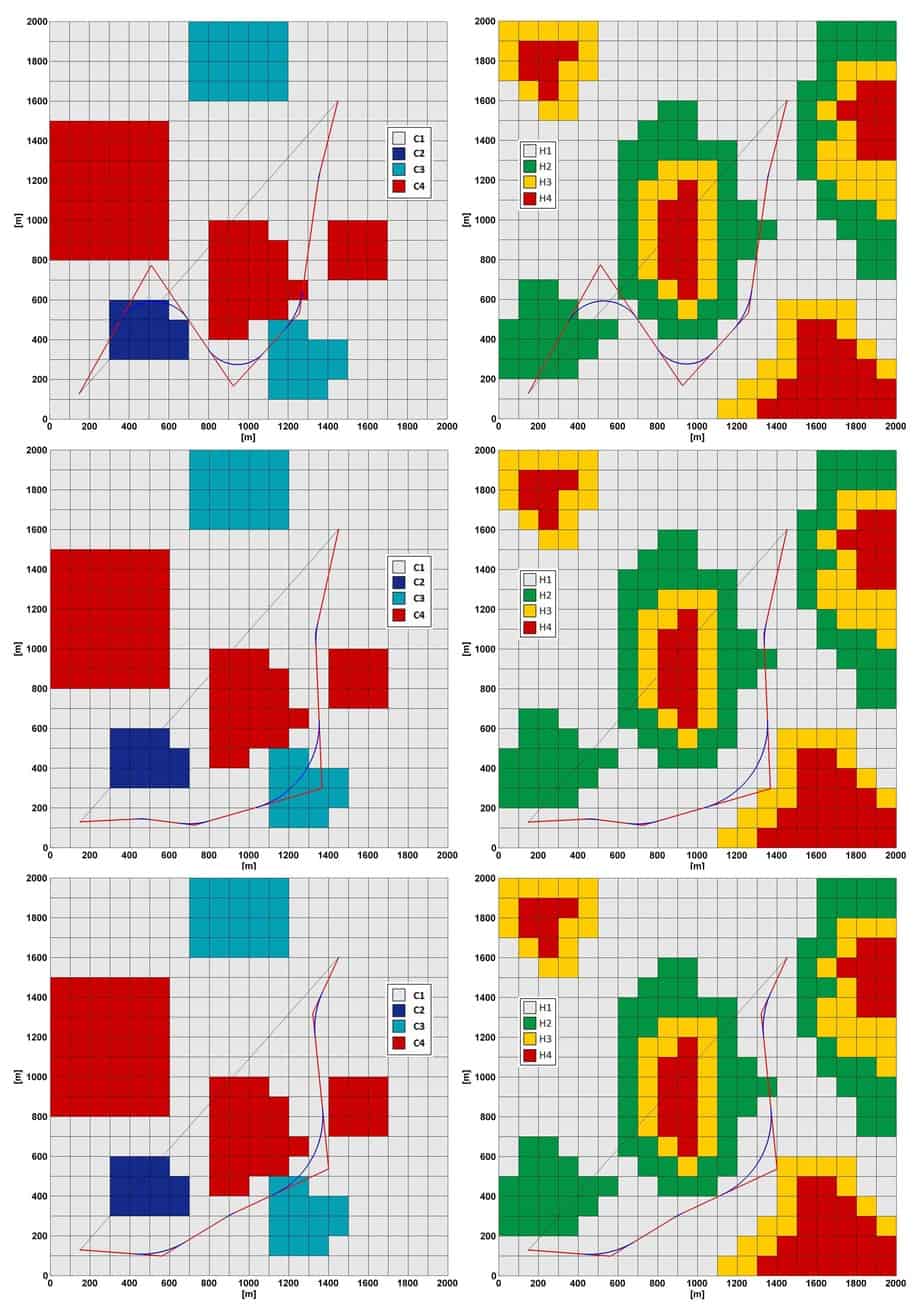
Si riportano i risultati del test maggiormente interessante. Le mappe di riferimento sono rettangolari con lati di 2.000 m. Il passo dx e dy è di 100 m. La matrice gridval è stata rappresentata attraverso 4 valori di riferimento per il costo di attraversamento unitario di ogni singola cella (da C1 basso a C4 altissimo), rappresentativo delle caratteristiche meccaniche del terreno e del valore dell’area. La mappa di pericolosità ambientale è caratterizzata da quattro livelli di pericolosità (da P1 basso a P4 molto alto), cui viene poi associato un diverso valore di penalità di base. Definite tutte le variabili di calcolo (quattro vertici, 50 individui, 1.000 cicli, Vmax = 450 m, w = 0,5, c1 = 1,5, c2 = 2,5), i costi e le penalità è stato possibile eseguire i test.
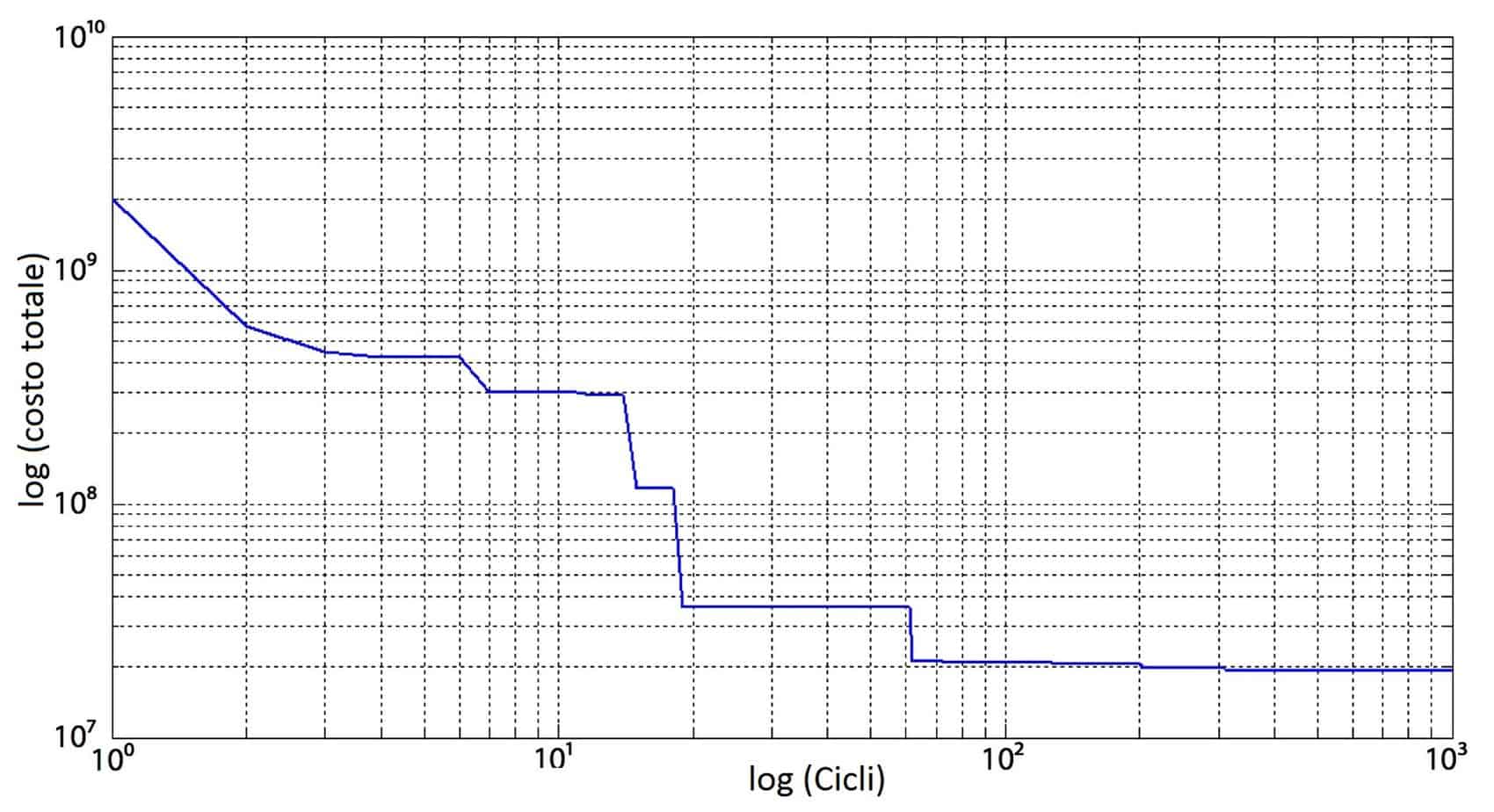
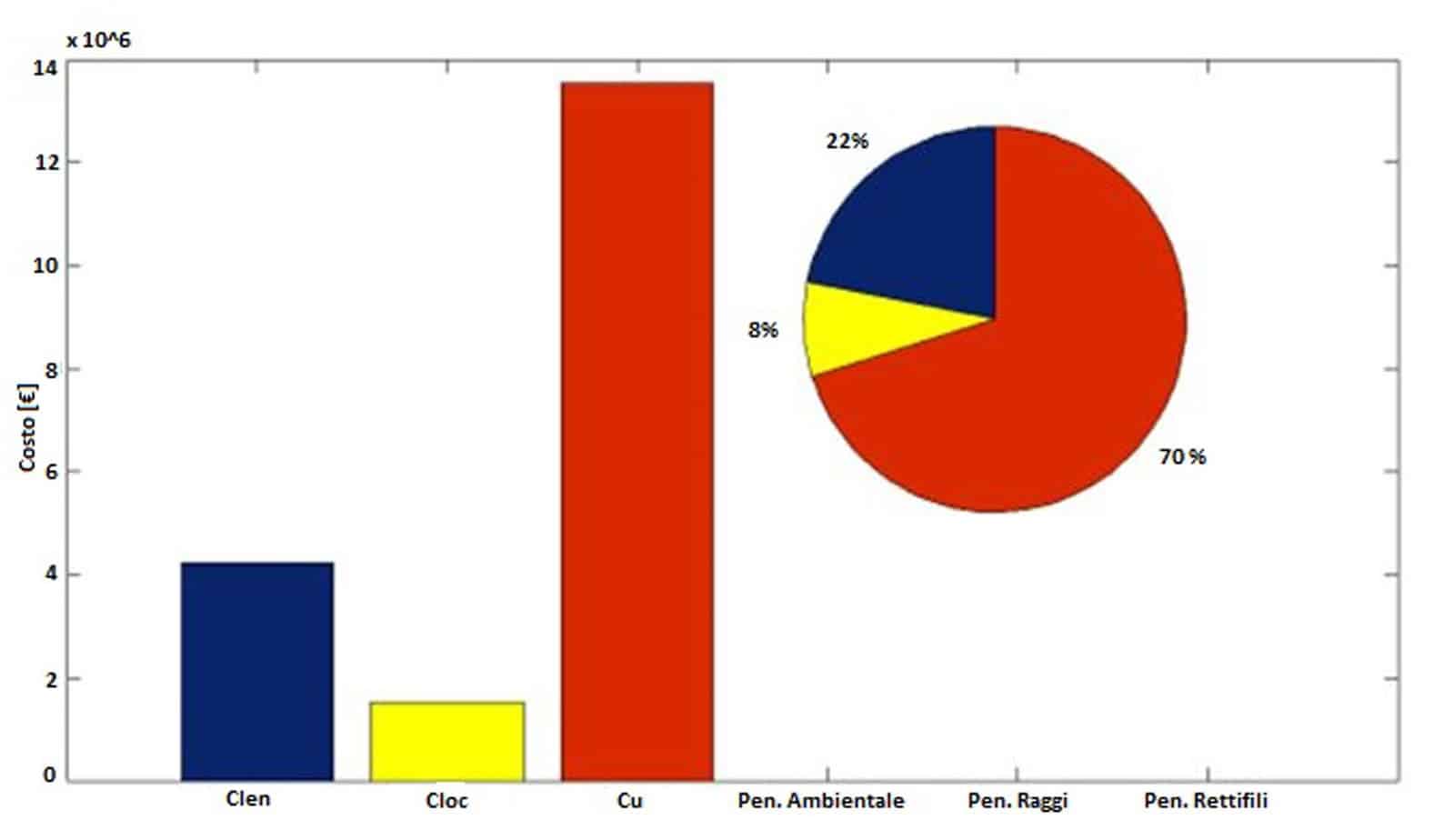
Si riportano i migliori tracciati trovati dopo 10, 200 e 1.000 cicli. Da una analisi delle figure, è possibile visualizzare l’effettiva evoluzione del tracciato e il sempre maggiore adattamento del percorso alla tortuosità dell’area di studio: il tracciato finale evita le celle caratterizzate da costi elevati e le aree ad alta pericolosità. Si può evidenziare l’effettiva minimizzazione del costo del tracciato, diagrammando il costo della migliore soluzione in funzione del numero dei cicli in scala logaritmica. Può essere interessante anche il confronto tra le diverse voci di costo: le penalità risultano nulle a conferma della correttezza della soluzione; inoltre i costi per gli utenti hanno una incidenza maggiore poiché sono rapportati all’intera vita utile prevista per l’infrastruttura.
Conclusioni
In questo studio è stata sviluppata una procedura basata sul PSO per ottimizzare il progetto geometrico di un tracciato stradale considerando i diversi vincoli presenti sul territorio. Nell’algoritmo di ottimizzazione sono state introdotte le funzioni di costo relative alle voci di costruzione e manutenzione dell’infrastruttura, di stabilizzazione dei suoli e di esproprio delle aree e quelle relative alle spese sostenute dagli utenti direttamente e indirettamente.
La procedura risulta utile in fase di pianificazione del sistema infrastrutturale, per la definizione preliminare dei nuovi tracciati, ma può essere fondamentale anche per ottimizzare eventuali adeguamenti di strade esistenti che insistono su territori caratterizzati da livelli di pericolosità elevati, tali da compromettere sicurezza e funzionalità dell’opera in caso di evento critico.