La prima parte dell’articolo, proposta sul fascicolo n° 145 Gennaio/Febbraio 2021 a pag. 92, è online su https://www.stradeeautostrade.it/ponti-e-viadotti/requisiti-prestazionali-e-criteri-costruttivi-del-ponte-genova-san-giorgio-prima-parte/ mentre la seconda, pubblicata sul fascicolo n° 146 Marzo/Aprile 2021 a pag. 78, è online su https://www.stradeeautostrade.it/ponti-e-viadotti/requisiti-prestazionali-e-criteri-costruttivi-del-ponte-genova-san-giorgio-seconda-parte/.
Questo è il terzo di una serie di articoli inerenti la progettazione del ponte Genova San Giorgio, un’opera di grande impegno ma, soprattutto, soggetta a vincoli temporali, operativi e comunicativi, non comuni nella costruzione di un viadotto di tali dimensioni.
Tale relazione, che trovate sul fascicolo n° 147 Maggio/Giugno 2021 a pag. 62, descrive sinteticamente le analisi di risposta sismica locale effettuate per la progettazione del viadotto che sono state cruciali per la definizione di azioni e spostamenti dimensionanti sia per la struttura sia per le verifiche di stabilità dei versanti della valle.
La scelta di utilizzare un modello non-lineare per la risoluzione del problema ha concesso duttilità nella gestione di un iter progettuale difficilmente prevedibile a-priori. Nella presentazione dei risultati delle simulazioni, grande attenzione è posta sulla caratterizzazione geotecnica alla base del modello numerico.
L’analisi di risposta sismica locale per il ponte
La progettazione del ponte Genova San Giorgio ha richiesto un’attenta valutazione dell’azione sismica attesa al sito [1]. È noto infatti come gli effetti di sito possano influenzare in modo drammatico intensità e distribuzione del moto sismico in superficie [2].
Per analisi di risposta sismica locale si intende proprio la valutazione quantitativa delle modifiche subite dal segnale in condizioni di campo libero. Le modifiche del moto sismico dovute alla morfologia irregolare del substrato roccioso riscontrata nel bacino della Val Polcevera (Figura 1) sono state investigate attraverso una modellazione numerica più complessa di quella generalmente richiesta in una progettazione “convenzionale”.
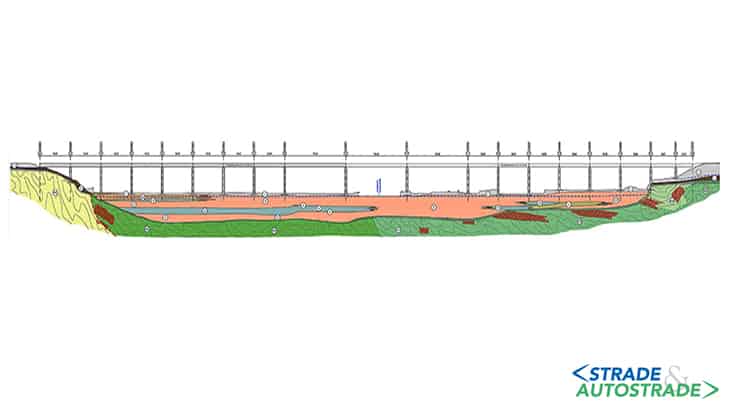
La caratterizzazione geotecnica utilizzata nel modello numerico è basata su una robusta campagna di indagini di sito che ha permesso di ricostruire con precisione:
- geometria e litostratigrafia delle unità geotecniche;
- morfologia dell’interfaccia “deposito alluvionale-substrato roccioso”;
- parametri meccanici dei materiali.
Il presente lavoro ha come obiettivo quello di illustrare alcuni risultati delle simulazioni numeriche. Particolare attenzione è poi posta sull’analisi degli effetti topografici, riscontrati nel presente caso, tipici dei bacini superficiali [3], il cui comportamento sismico è essenzialmente governato da fenomeni bidimensionali.
Il modello di calcolo
Per descrivere compiutamente il comportamento meccanico dei terreni soggetti a condizioni di carico cicliche è adottato un modello costitutivo di tipo isteretico.
Il modello utilizzato segue l’effettivo percorso tensioni-deformazioni durante le condizioni di carico ciclico tenendo implicitamente conto:
- della non-linearità degli sforzi;
- dell’irreversibilità delle deformazioni;
- della dissipazione di energia, introdotta utilizzando uno smorzamento di tipo isteretico.
Il problema bidimensionale in oggetto è risolto mediante il metodo alle differenze finite con il codice FLAC [4].
Geometria, condizioni al contorno e parametri meccanici
Il dominio di calcolo, composto da circa 24.000 nodi, è illustrato in Figura 2 con le rispettive condizioni al contorno. Le dimensioni del dominio (2.450 m x 185 m) sono scelte sia in funzione della lunghezza del ponte sia in modo tale da poter ragionevolmente escludere modifiche parassite del segnale all’interno del bacino stesso. In figura si riporta, inoltre, una rappresentazione schematica del ponte non oggetto delle simulazioni presentate.
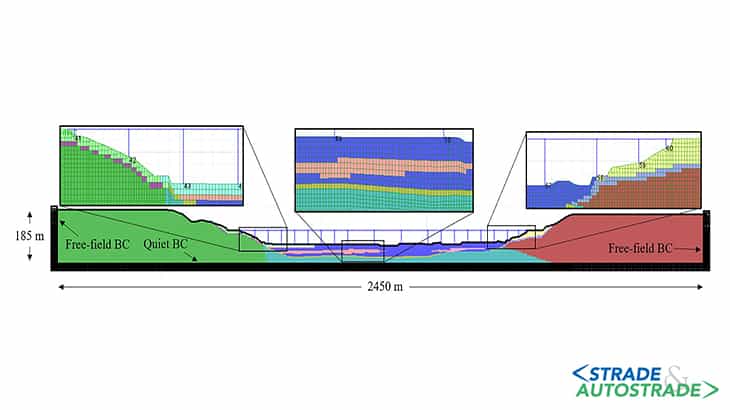
Per quanto concerne le condizioni al contorno alla base, al fine di rappresentare un semi-spazio, sono applicati dei contorni assorbenti composti da smorzatori indipendenti per le due direzioni del moto (“Quiet BC” in Figura 2). Per i contorni laterali si adottano condizioni di tipo free-field, il cui utilizzo è largamente diffuso in ambito numerico proprio per la loro efficacia dimostrata in modelli agli elementi e alle differenze finite [5].
Per un’accurata modellazione della propagazione di un’onda attraverso il dominio, la dimensione degli elementi della griglia deve essere contenuta in una frazione della lunghezza d’onda associata alla frequenza più elevata della sollecitazione dinamica applicata [6].
Note dunque le caratteristiche di rigidezza del terreno e il contenuto in frequenza del segnale applicato, si definisce una griglia numerica in grado di simulare accuratamente il fenomeno dinamico in esame.
La distanza massima tra i nodi della griglia (< 4,17 m) è quindi tarata al fine di descrivere efficacemente segnali con frequenza massima di 8 Hz. Tale frequenza risulta sufficiente a coprire i periodi di interesse superiori a 0,15 s.
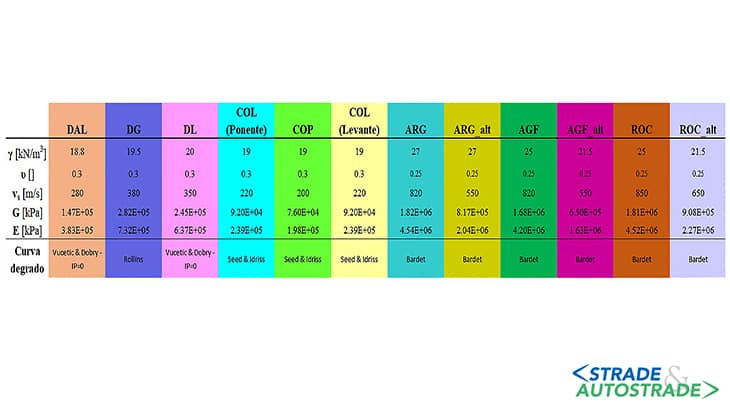
Per i terreni in sito, in Figura 3 si riportano, per ogni materiale, i parametri meccanici adottati nel modello numerico. I colori dei materiali sono coerenti con quelli della discretizzazione rappresentata in Figura 1.
I parametri sono presi in accordo con i risultati della campagna di indagini condotta in sede di progettazione esecutiva. Nell’ultima riga della Figura 3, si esplicita, inoltre, il corrispondente modello di degrado adottato. Per l’implementazione delle curve di degrado è utilizzato il modello sigmoidale a tre parametri (“sig3” nel codice di calcolo [4]).
La taratura dei parametri del modello di degrado è effettuata iterativamente, in maniera da ottenere il miglior accordo tra le curve di letteratura e il modello sigmoidale in termini di curva di decadimento della rigidezza e curva di smorzamento.
La campagna indagini di laboratorio ha visto, inoltre, la realizzazione di specifiche prove per la definizione di degrado del modulo di rigidezza dei terreni in presenza di sollecitazioni cicliche. In particolare, sono state eseguite sei prove triassiali cicliche e 12 prove di colonna risonante.
È quindi possibile confrontare i risultati delle prove dinamiche cicliche con curve di letteratura adottate nei modelli di degrado. A titolo rappresentativo, si presentano due dei confronti effettuati:
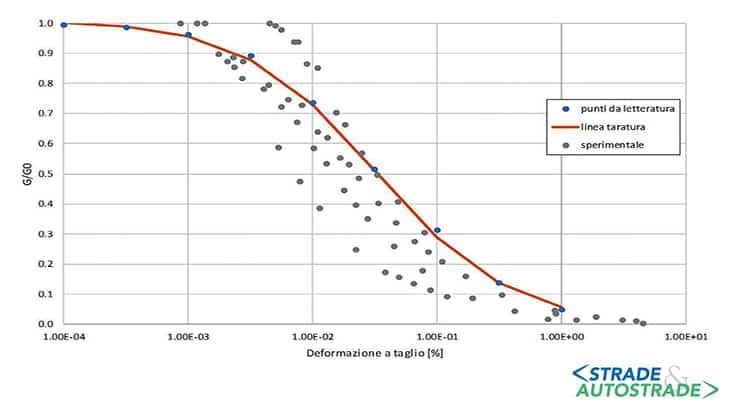
- per l’unità che comprende i depositi ghiaiosi (DG) in Figura 4 sotto, si riporta il confronto tra i dati di quattro prove triassiali cicliche con la curva suggerita da Rollins (1998) per gli stessi terreni;
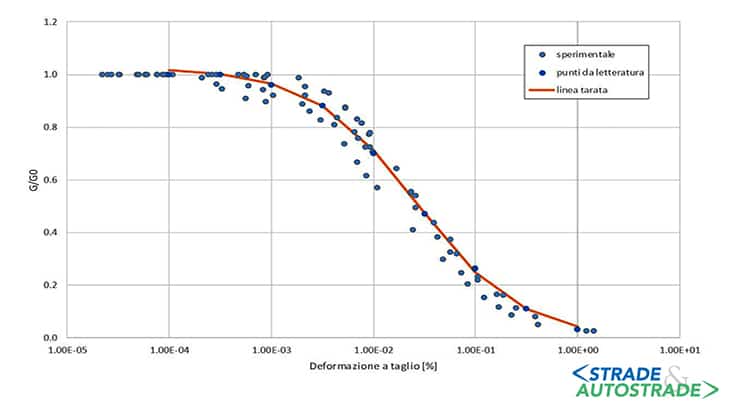
- per i depositi fluviali (DAL) in Figura 5 sotto, si riporta il confronto tra i dati di cinque prove di colonna risonante con la curva suggerita da Vucetic e Dobry (1991).
Si può quindi osservare come vi sia un ottimo accordo tra i risultati sperimentali e le curve di letteratura utilizzate nelle analisi per la simulazione del comportamento dinamico dei terreni.
I segnali in input
Ai vincoli alla base del modello è imposta una storia temporale in termini di accelerazione orizzontale e verticale. In modo conforme a quanto indicato dalle Normative tecniche [1], le analisi sono condotte imponendo sette storie accelerometriche (spettrocompatibili con uno spettro target) ricavate da altrettanti accelerogrammi naturali.
Tali registrazioni sono selezionate utilizzando il database PEER (http://ngawest2.berkeley.edu). Lo spettro target utilizzato è definito dalla Normativa su suolo rigido affiorante orizzontale per un periodo di ritorno pari a 1.898 anni con coefficiente di smorzamento del 5%.
Per la verifica di compatibilità spettrale, gli accelerogrammi naturali sono opportunamente scalati linearmente nel dominio del tempo con un fattore massimo di scala pari a 5.
Al fine di cogliere gli effetti del sistema analizzato sia alle basse che alle alte frequenze, lo spettro di risposta medio del set di registrazioni selezionate è compatibile con lo spettro target di progetto in un intervallo di 0,15-4,00 s.
All’interno di tale intervallo, lo scarto in difetto e in eccesso tra lo spettro target e lo spettro medio del set è compreso, rispettivamente, tra il 10% e il 30%. Ulteriori dati di input richiesti per la selezione dei segnali sono i parametri che determinano la pericolosità sismica del sito.
In questo studio sono utilizzati magnitudo e distanza epicentrale. I valori limite di queste grandezze sono ottenuti utilizzando i risultati della disaggregazione della pericolosità sismica per il sito di interesse (www.esse1-gis.mi.ingv.it).
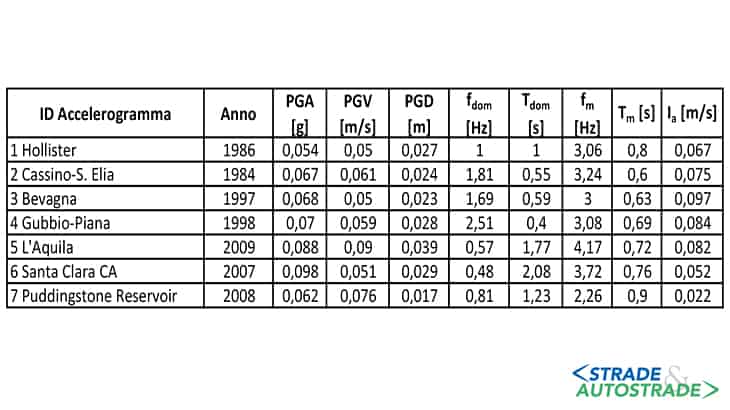
Gli accelerogrammi individuati sono quindi deconvoluti e trasposti in velocigrammi al fine di consentirne l’implementazione in FLAC attraverso i vincoli alla base. Si riportano in Figura 6 i segnali orizzontali in input e i relativi parametri rappresentativi e sono quindi riportate accelerazione, velocità e spostamento di picco dei segnali (PGA, PGV e PGD, rispettivamente).
Sono inoltre illustrate la frequenza e il periodo dominante (fdom e Tdom) accanto a frequenza quadratica media (fm) e periodo quadratico medio (Tm). Nell’ultima colonna è infine riportata l’intensità di Arias (Ia).
Le storie verticali in accelerazione imposte alla base del dominio corrispondono alle componenti verticali delle registrazioni naturali. La spettrocompatibilità dei segnali verticali è quindi imposta rispetto al corrispondente spettro verticale normativo.
I risultati numerici
I risultati qui illustrati si riferiscono principalmente all’accelerogramma 6 che esibisce la PGA orizzontale più alta rispetto agli altri segnali selezionati in input.
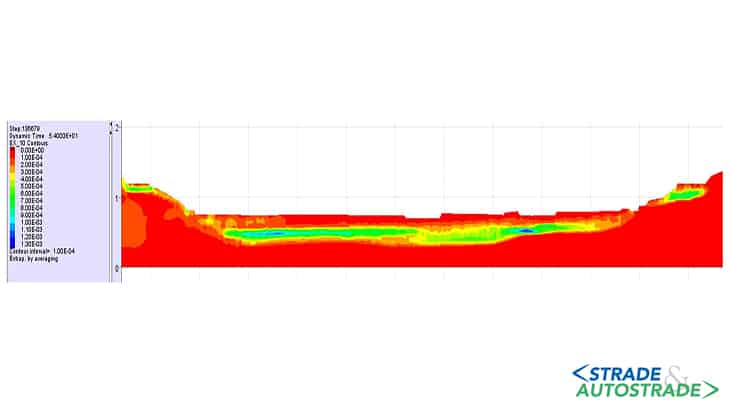
In Figura 7 sotto si riporta l’inviluppo della deformazione a taglio calcolato in termini di distribuzione spaziale per il sisma n° 6. I valori di deformazione massima si verificano all’interfaccia tra substrato e deposito nella porzione centrale del bacino (0,1%-0,01%) e in corrispondenza delle coltri poste sui rilievi di Levante e Ponente (0,05%-0,01%). Valori modesti di deformazione a taglio si notano invece in corrispondenza della superficie e del substrato più rigido (< 0,01%).
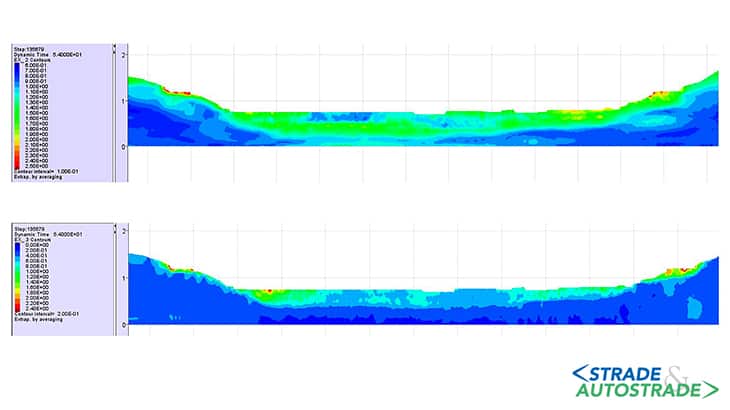
I corrispondenti risultati in termini di massima accelerazione orizzontale e verticale sono riportati, rispettivamente, negli inviluppi mostrati nelle Figure 8A e 8B sotto.
In corrispondenza delle coltri poste sui rilievi laterali si notano valori di accelerazione orizzontale e verticale nel range di 1,00 m/s2-2,50 m/s2. Nella parte centrale del deposito, in prossimità dell’affioramento del substrato (a sinistra in Figura 8B sotto), è facilmente verificabile come il valore di accelerazione verticale sia più elevato, in modulo, rispetto a quello calcolato per l’accelerazione orizzontale.
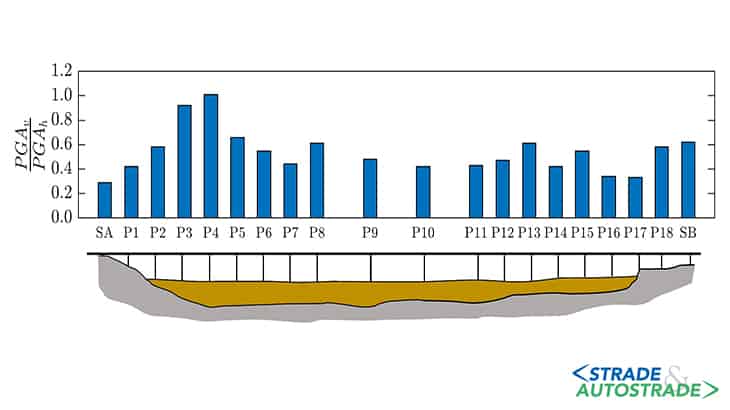
Si riscontra un’accelerazione verticale fino a 2,40 m/s2 rispetto a un valore di quella orizzontale incluso nel range 1,20 m/s2-2,00 m/s2. Per indagare quest’ultimo aspetto, si riporta in Figura 9 sotto il corrispondente rapporto di amplificazione, definito come il rapporto tra PGA verticale (PGAv) e PGA orizzontale (PGAh), calcolato a piano campagna in corrispondenza delle sottostrutture del ponte Genova San Giorgio.
In basso, sempre in Figura 9, viene rappresentato il profilo geotecnico semplificato, la cui attenzione è posta unicamente sulla morfologia dell’interfaccia “deposito superficiale-substrato roccioso”.
Si sottolinea come in tale grafico il rapporto di amplificazione cresca sino a superare il valore dell’unità nella pila 4. Tale effetto, riscontrato anche per i risultati relativi gli altri accelerogrammi qui non mostrati per brevità, sembra essere dovuto essenzialmente alla focalizzazione delle onde sismiche in aree prossime al bordo del bacino.
È infatti noto come la focalizzazione di tali onde sia associata all’interferenza tra onde incidenti e molteplici riflessioni che avvengono in aree prossime al bordo della valle [7].
La conformazione geometrica dell’interfaccia deposito-bedrock in corrispondenza del bordo sinistro della valle è evidente come incentivi proprio la focalizzazione dei segnali sismici verso le pile 3 e 4. Infine, questo fenomeno produce una risposta sismica marcatamente differente lungo la superficie del bacino e, dunque, lungo il ponte stesso.
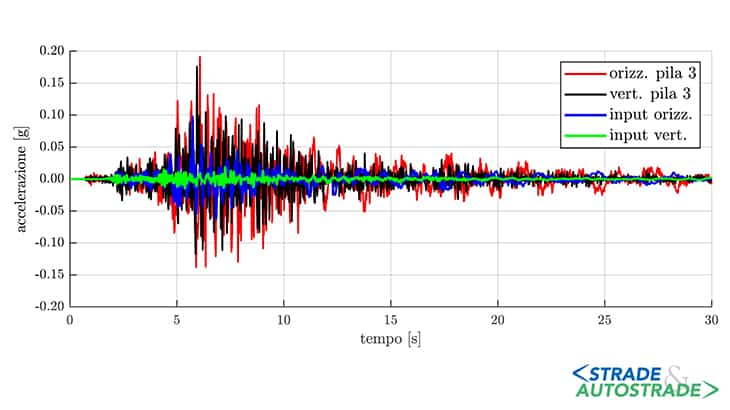
Per il sisma n° 6, in Figura 10 si riporta il confronto tra i segnali in input e quelli ottenuti dalle analisi numeriche per la pila 3 in termini di accelerazione orizzontale e verticale. È evidente come l’amplificazione sismica verticale sia di molto superiore a quella relativa all’accelerazione orizzontale.
Risulta infatti per la PGA verticale un incremento del 640% rispetto al segnale in input (0,027 g in input contro 0,175 g in output) a fronte di un aumento del 169% per la PGA orizzontale (0,113 g in input contro 0,191 g in output).
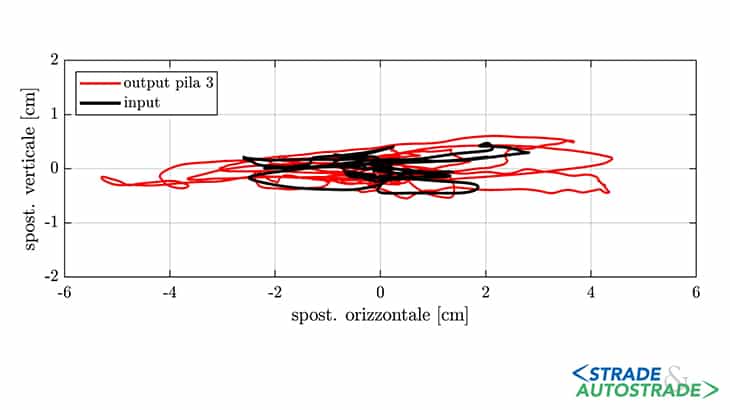
Il confronto tra segnali in input e segnali calcolati in output in termini di spostamento è visibile nell’odogramma illustrato in Figura 11, ove è rappresentato il vettore spostamento calcolato per ogni istante temporale nel piano contenente il modello di calcolo (Figura 1).
Si evidenzia, infine, come per il segnale in input lo spostamento totale massimo è di circa 3,0 cm mentre per i risultati in output lo spostamento massimo è prossimo ai 5,5 cm.
Conclusioni
Il presente lavoro ha riguardato lo studio della risposta sismica locale della Val Polcevera. Le analisi condotte hanno permesso di valutare in modo puntuale le modifiche del moto sismico in corrispondenza delle sottostrutture del ponte Genova San Giorgio. Particolare attenzione è stata posta sull’analisi del comportamento sismico, prevalentemente bidimensionale, del bacino.
A valle di questo studio, sono stati effettuati confronti quantitativi con il metodo semplificato di valutazione degli effetti di sito proposto dalla Normativa tecnica [1]. Tali confronti hanno infine consentito di individuare le azioni sismiche progettualmente dimensionanti per la struttura in elevazione.
Bibliografia
[1]. Decreto Ministeriale del 17/01/2018: “Aggiornamento delle Norme tecniche per le costruzioni”, GU n° 42 del 20 Febbraio 2018, Suppl. Ordinario n° 8.
[2]. S.L. Kramer – “Geotechnical earthquake engineering”, Pearson Education India, 1996.
[3]. P.Y. Bard, M. Bouchon – “The two-dimensional resonance of sediment-filled valleys”, Bulletin of the Seismological Society of America 75.2, 1985, 519-541.
[4]. Itasca, F.L.A.C. – “Fast Lagrangian analysis of continua”, Itasca Consulting Group Inc., Minneapolis, Minn., 2000.
[5]. P.A. Cundall et al. – “NESSI, soil structure interaction program for dynamic and static problems”, Norwegian Geotechnical Institute, Report (1980): 51508-9.
[6]. J. Lysmer, R.L. Kuhlemeyer – “Finite Dynamic Model for Infinite Media”, J. Eng. Mech., 95(EM4), 859-877, 1969.
[7]. F. Gelagoti, R. Kourkoulis, I. Anastasopoulos, T. Tazoh, G. Gazetas – “Seismic wave propagation in a very soft alluvial valley: sensitivity to ground-motion details and soil nonlinearity, and generation of a parasitic vertical component”, Bulletin of the Seismological Society of America, 100(6), 3035-3054, 2010.
La prima parte dell’articolo, proposta sul fascicolo n° 145 Gennaio/Febbraio 2021 a pag. 92, è online su https://www.stradeeautostrade.it/ponti-e-viadotti/requisiti-prestazionali-e-criteri-costruttivi-del-ponte-genova-san-giorgio-prima-parte/ mentre la seconda, pubblicata sul fascicolo n° 146 Marzo/Aprile 2021 a pag. 78, è online su https://www.stradeeautostrade.it/ponti-e-viadotti/requisiti-prestazionali-e-criteri-costruttivi-del-ponte-genova-san-giorgio-seconda-parte/.
> Se questo articolo ti è piaciuto, iscriviti alla Newsletter mensile al link http://eepurl.com/dpKhwL <