Questo primo articolo tratta le caratteristiche che influenzano il comportamento delle Gerber agli stati limite ultimi: dopo una breve introduzione, sono presentati e applicati a un caso studio due modelli di calcolo della resistenza ultima della Gerber (www.masera-eg.it).
In un prossimo fascicolo verranno illustrate le caratteristiche che influenzano il comportamento delle selle Gerber in esercizio, sempre trattando il caso studio illustrato.
Nel caso di strutture in calcestruzzo ordinario o precompresso, le selle Gerber (half-joint o dapped-end in inglese) formano gli appoggi di una trave Gerber, che prende il suo dall’inventore Heinrich Gottfried Gerber.
Tale elemento strutturale venne spesso utilizzato negli anni 1960-1980 in ponti e viadotti poiché essi potevano beneficiare dell’introduzione di uno schema isostatico anche in casi di strutture continue e l’altezza totale della struttura veniva minimizzata (Figura 1).
Per quest’ultimo motivo, giunti analoghi sono spesso utilizzati anche nell’edilizia, ove sia necessario ottimizzare l’altezza totale, come in strutture sotterranee o industriali.
Le problematiche legate alle selle Gerber
Nonostante la grande diffusione negli anni 1960-1980, negli ultimi anni è stato riconosciuto il problema costituito da questi elementi. Riferendosi al periodo di progetto ed esecuzione della maggior parte di essi, i carichi stradali sono aumentati, i codici sono cambiati anche in vista di una maggior conoscenza dei materiali e delle problematiche ad essi associate.
Anche in caso di costruzioni conformi alle attuali Norme, effetti ambientali e accidentali causano un inevitabile degrado dei materiali e degli elementi.
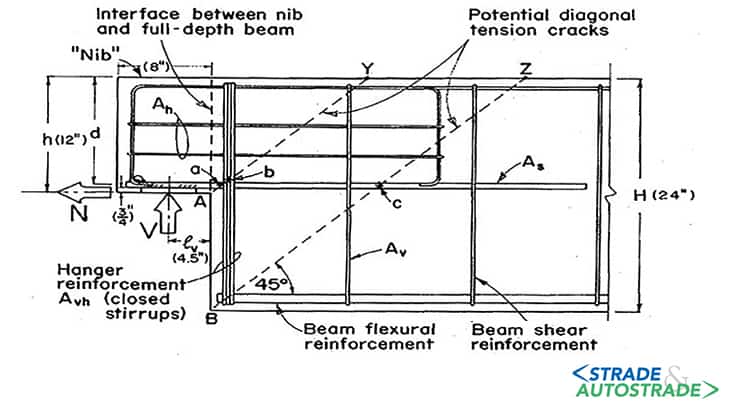
La geometria del giunto, fautrice dei pregi che ne hanno causato la diffusione, è causa delle maggiori preoccupazioni che sono ad esso legato:
- l’acqua proveniente dalla pavimentazione stradale ha una corsia preferenziale che permette la diretta penetrazione e ristagno nelle parti più sensibili, causando un inevitabile deterioramento dei materiali. Studi condotti in Inghilterra mostrano una riduzione di armatura fino al 50% all’interno della risega, risultando in una riduzione di resistenza limite fino al 35% [1];
- la sezione trasversale ridotta è un elemento tozzo di discontinuità, nel quale la diffusione delle tensioni non segue le leggi degli elementi unidimensionali. La rottura di tali elementi è a taglio, quindi fragile e immediata.
La particolarità di generare schemi statici isostatici ha lo svantaggio intrinseco di non conservare alcuna ridondanza; quindi, al crollo di una singola parte consegue il crollo dell’intera struttura.
Gli eventi catastrofici legati alle Gerber
Gli ultimi anni sono stati caratterizzati da eventi funesti legati al collasso di ponti e viadotti. Alcuni di essi furono conseguenza diretta del raggiungimento e superamento della resistenza limite della Gerber: i cavalcavia La Concorde (2006, Canada) e di Annone (2016, Italia), che hanno rispettivamente causato cinque e una vittima.
Nel caso de La Concorde, i codici in vigore al momento di progetto e costruzione non rendevano obbligatorio l’utilizzo di armatura resistente al taglio, se alcuni parametri venivano rispettati. Infatti, questo viadotto non era provvisto di armatura verticale e alcuni difetti di costruzione hanno causato le condizioni favorevoli alla formazione della fessura che ha portato al cedimento del giunto soggetto al solo peso proprio [2] in Figura 2 sopra.
A causa dalla ridotta altezza utile del viadotto Annone (inferiore ai 5 m), esso fu soggetto a svariati impatti di camion contro l’intradosso della trave di bordo, rendendo necessarie diverse riparazioni. Il collasso (riportato in Figura 3 sopra) non fu causato da un impatto ma dal passaggio di un mezzo pesante.
Nel progetto del 1962, il carico variabile sulla singola corsia era di 55 t, e secondo i codici in vigore al tempo del collasso la stessa categoria di viadotti avrebbe dovuto sostenere 92 t, ma il peso del mezzo che ha causato la rottura della Gerber era oltre le 107 t [3].
Questi due esempi mostrano chiaramente come carichi critici e codici non idonei possono causare rotture inevitabili se accompagnati da una gestione inadeguata delle infrastrutture.
Un appropriato piano di verifica e manutenzione deve essere attuato sulla maggioranza della rete infrastrutturale italiana; quindi, per permettere un efficace discretizzazione delle azioni devono essere identificate le opere più vulnerabili, anche secondo le indicazioni delle Linee Guida 2020 [4].
I modelli presentati in questo articolo nascono appunto con l’obiettivo di fornire uno strumento di vasta applicazione per la pianificazione della rete infrastrutturale.
I parametri di progetto che influenzano la resistenza delle Gerber
Intorno agli anni 1970-1980, al centro della ricerca inerente alle selle Gerber vi era l’ottimizzazione della disposizione delle armature e della geometria, per una vita utile e resistenza maggiori.
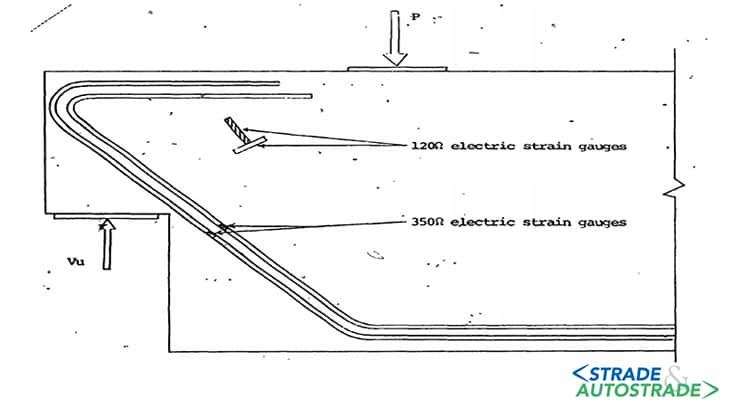
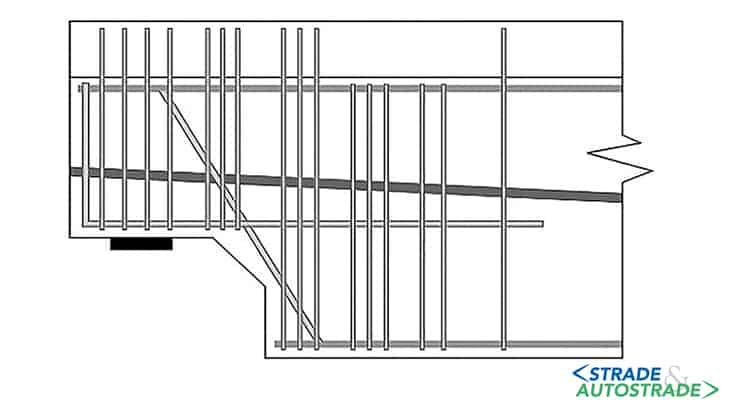
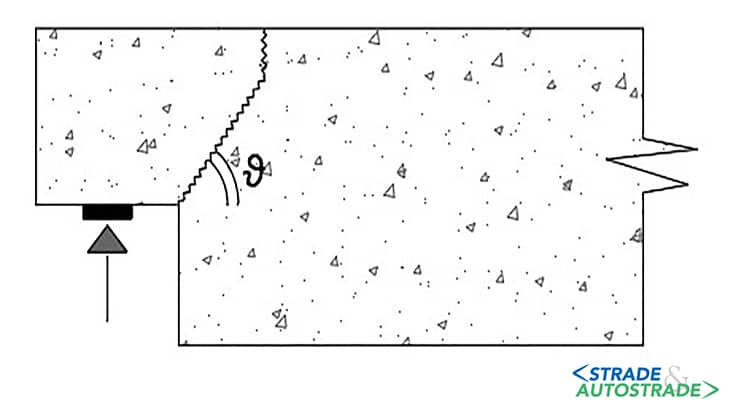
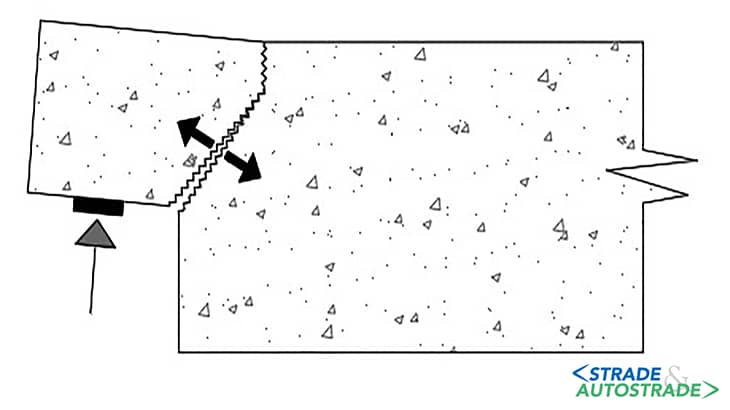
I primi studi furono fatti osservando la formazione e sviluppo delle fessure critiche [6] in Figura 4 sopra, identificando prima il layout ortogonale delle armature (Figura 5 sopra), e successivamente la necessità della barra diagonale, secondo uno studio condotto [7] riportato in Figura 6 sopra.
Un ulteriore fattore geometrico che ha influenzato le scelte progettuali delle selle Gerber definisce la forma dell’angolo della risega: se di 90° essa causa più facilmente la formazione di fessure, al contrario se fosse divisa un più segmenti (Figura 7 sopra).
I modelli tirante-puntone
I modelli tirante-puntone (strut and tie) rappresentano un classico metodo che permette di trattare punti di discontinuità in cui le ipotesi di Bernoulli non possono essere considerate valide, quindi la teoria della trave non è applicabile.
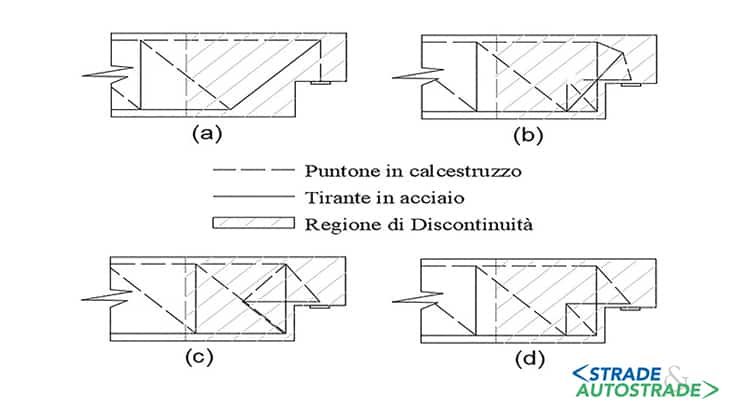
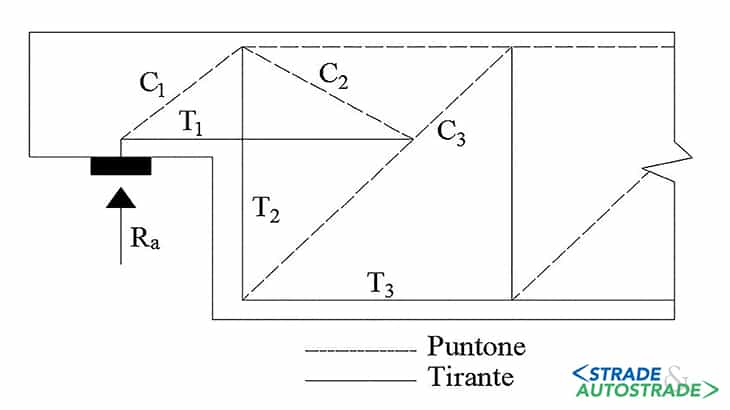
Rappresentano una schematizzazione del flusso di tensioni all’interno dell’elemento di discontinuità, sottoforma di una reticolare formata da elementi compressi in calcestruzzo (puntoni) ed elementi tesi in acciaio (tiranti), uniti da nodi (Figura 8).
Tali reticolari furono spesso utilizzate per il calcolo della resistenza ultima delle selle Gerber [8]. È da sottolineare però che questo metodo è a tutti gli effetti un’applicazione del Teorema del limite inferiore, quindi sottostima la reale resistenza dell’oggetto. In funzione dell’armatura presente nell’elemento è possibile, in fase di verifica del giunto, utilizzare uno o più modelli esistenti.
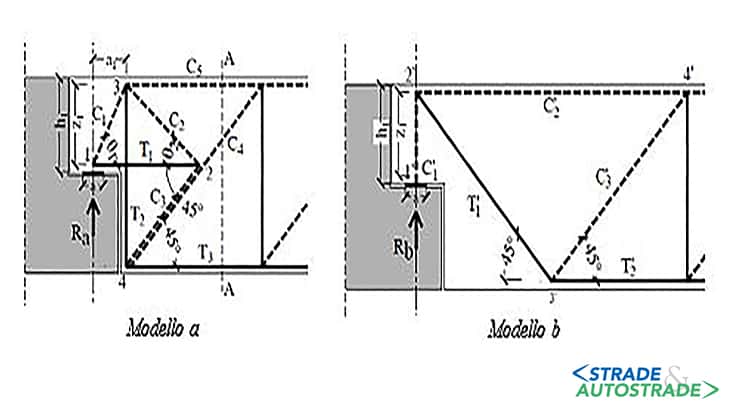
Nei paragrafi successivi, è presentato un caso studio analizzato con un modello tirante-puntone, ottenuto tramite la sovrapposizione di due reticolari come proposto da Clark e Thorogood nel 1988 [9], analizzato nei particolari da R. Asso (2020) [10].
I due modelli rappresentati in Figura 9 sono complementari: infatti, le armature utilizzate sono diverse a seconda del modello a o modello b e i percorsi delle tensioni sono anch’essi indipendenti.
Da sottolineare che il modello a viene attivato con la presenza di armature orizzontali nella risega e verticali nella sezione piena, mentre il modello b sfrutta l’armatura diagonale di Liem. Tramite un procedimento iterativo è possibile definire le resistenze delle due reticolari, la cui somma rappresenta la resistenza del giunto stesso.
Per una completezza di analisi è riportato anche un secondo modello di calcolo della resistenza della trave, basato su un cinematismo (ipotesi di formazione di una fessura) rappresentato nelle Figure 10A e 10B sopra. Questo secondo modello identifica un limite superiore di resistenza del giunto.
Il caso studio
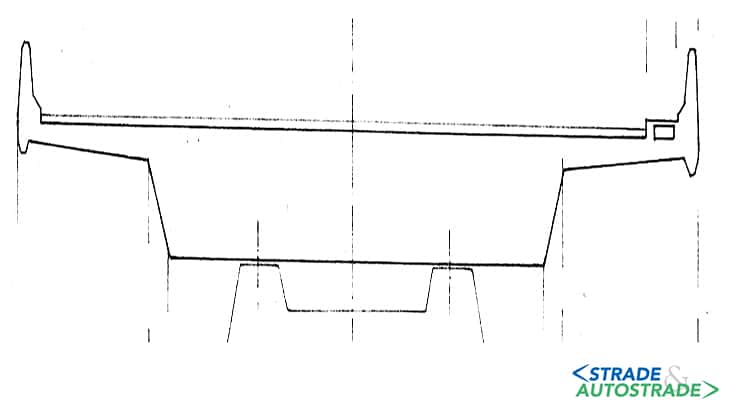
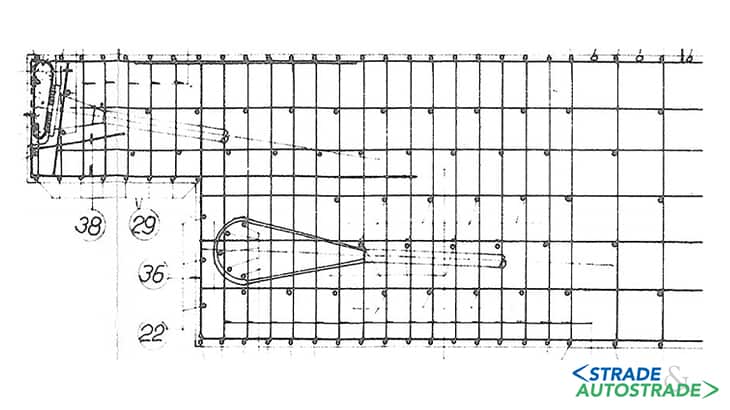
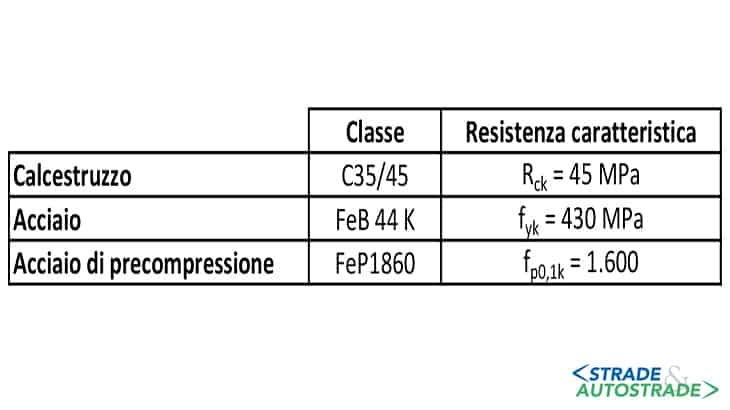
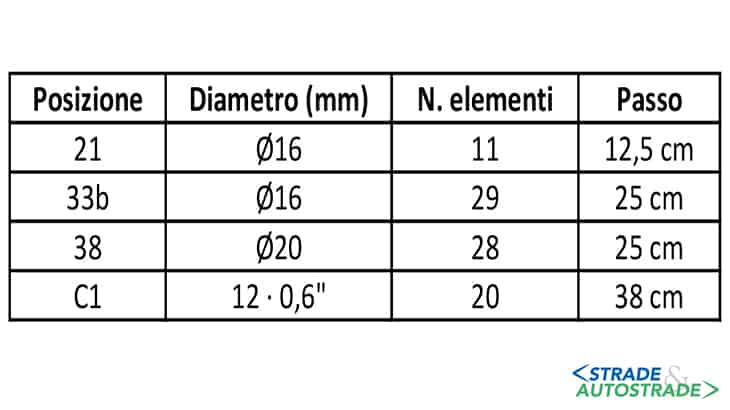
Il caso studio proposto tratta il giunto Gerber presente in un viadotto a cassone pieno (Figure 11A e 11B), le cui caratteristiche sono riportate nelle Figure 12 e 13.
Da un’analisi preliminare e con le conoscenze introdotte nei paragrafi precedenti, si può dedurre che l’assenza di armatura diagonale può risultare in una criticità per l’elemento, visto che il modello b non è attivato. Inoltre, la risega è a 90°, quindi fornisce un contrasto limitato per quanto riguarda la formazione di fessure.
Il calcolo dei limiti di resistenza
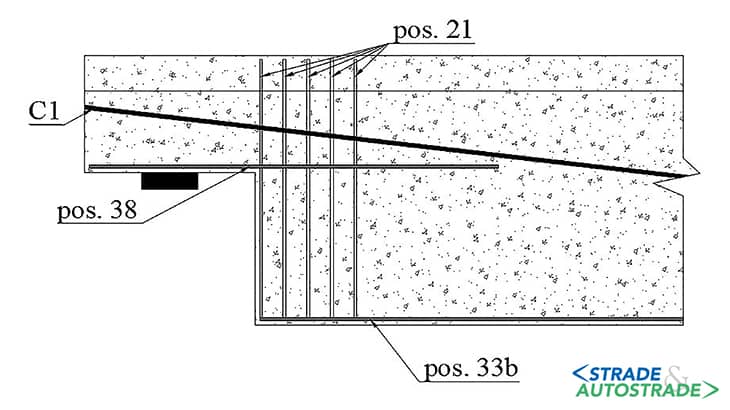
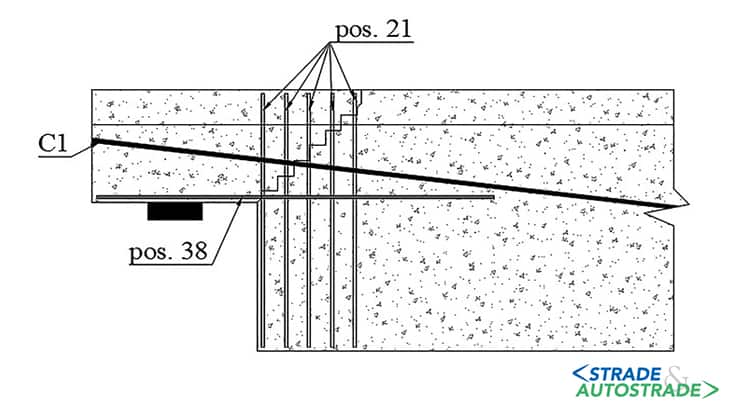
Nel calcolo del limite inferiore di resistenza entra in gioco soltanto l’armatura ortogonale (Figura 14). Secondo il modello proposto, essa giunge a rottura per snervamento del tirante T2 (Figure 15A e 15B), quindi una rottura a taglio duttile.
Per quanto riguarda il limite superiore, ipotizzando la formazione di una fessura nella risega è possibile andare a studiare le armature (lente e di precompressione) che contribuiscono alla sua chiusura, riassunte in Figura 14.
In funzione della posizione e classe degli elementi, viene identificato un meccanismo resistente, che indica un valore di solito più vicino ma eccedente il reale limite del giunto. Basandoci su informazioni provenienti da ispezioni effettuate da Personale tecnico, è stata imposta una fessura di 45° a partire dall’angolo della risega in Figura 17 sotto.
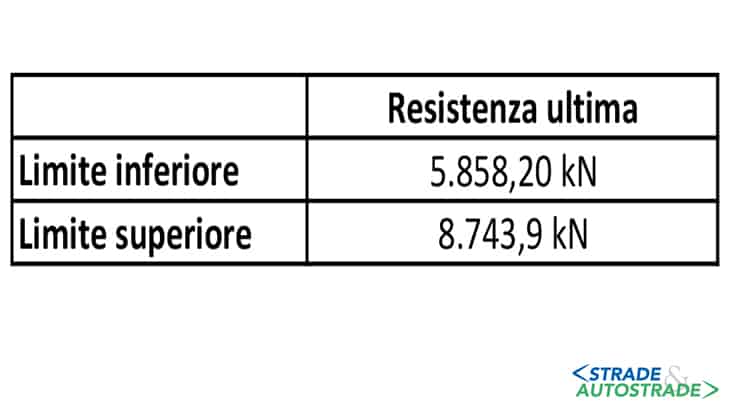
In seguito è riportata la Figura 18 sotto riassuntiva con le resistenze calcolate dai due modelli.
Conclusioni
Nell’articolo sono state presentate le caratteristiche principali delle selle Gerber, rischi e benefici che hanno portato questo particolare elemento a essere spesso utilizzato nella costruzione di ponti, ma che attualmente rappresenta una criticità nel patrimonio strutturale.
Un caso studio di una sella Gerber appartenente a un impalcato a cassone pieno è stato utilizzato per applicare due modelli analitici per il calcolo di un limite inferiore e un limite superiore dell’elemento: il range così definito identifica la resistenza del giunto.
Bibliografia
[1]. P. Desnerck, J. M. Lees, C. T. Morley – “The effect of local reinforcing bar reductions and anchorage zone cracking on the load capacity of RC half-joints”, Eng. Struct., vol. 152, pp. 865-877, Dec. 2017, doi: 10.1016/j.engstruct.2017.09.021.
[2]. D. Mitchell, M. Asce, J. Marchand, P. Croteau, W.D. Cook – “Concorde Overpass Collapse: Structural Aspects,” ascelibrary.org, vol. 25, n. 6, pp. 545-553, Dec. 2011, doi: 10.1061/(ASCE)CF.1943-5509.0000183.
[3]. M. Di Prisco – “Critical infrastructures in Italy: State of the art, case studies, rational approaches to select the intervention priorities”, 2019, Accessed: Apr. 07, 2021, available: https://re.public.polimi.it/handle/11311/1157258.
[4]. “Linee Guida per la classificazione e gestione del rischio, la valutazione della sicurezza ed il monitoraggio dei ponti esistenti”, Ministero delle Infrastrutture e dei Trasporti, Consiglio Superiore dei Lavori Pubblici, 2020.
[5]. “Annone: in camera di commercio a Lecco l’udienza preliminare per il crollo del ponte – CasateOnline”, https://www.casateonline.it/articolo.php?idd=122033&origine=1&t=Annone%3A+in+camera+di+commercio+a+Lecco+l%27udienza+preliminare+per+il+crollo+del+ponte.
[6]. A.H. Mattock, T.C. Chan – “Design and Behavior of Dapped-End Beams”, accessed: Apr. 07, 2021. [Online]. Available: https://www.pci.org/PCI_Docs/Publications/PCI, Journal/1979/November-1979/Design and Behavior of Dapped-End Beams.pdf, 1979.
[7]. S.K. Liem – “Maximum shear strength of dapped-end or corbel”, 1983.
[8]. J. Schlaich, K. Schaefer, M. Jennewein – “Toward a consistent design of structural concrete”, PCI J., vol. 32, n. 3, pp. 74-150, 1987, doi: 10.15554/pcij.05011987.74.150.
[9]. L. Clark, P. Thorogood – “Serviceability behaviour of reinforced concrete half joints”, Struct. Eng., 1988, Accessed: Apr. 07, 2021, available: https://trid.trb.org/view/295410.
[10]. R. Asso – “Half-joint assessment of concrete bridges: strut and tie model development and FEM validation” Politecnico di Torino, Turin, 2020.
> Se questo articolo ti è piaciuto, iscriviti alla Newsletter mensile al link http://eepurl.com/dpKhwL <