La seconda parte dell’articolo è sul fascicolo n° 149 Settembre/Ottobre 2021 a pag. 57 e online su https://www.stradeeautostrade.it/ponti-e-viadotti/il-fenomeno-della-fatica-nei-ponti-in-acciaio-a-lastra-ortotropa-seconda-parte/.
Gli impalcati in lastra ortotropa hanno portato notevoli benefici per quanto riguarda la progettazione di ponti con grande luce. Allo stesso tempo, però, necessitano di un elevato numero di elementi saldati o bullonati tra loro, soggetti a continue variazioni di tensione, quindi sollecitati a fatica.
Nel seguente articolo verrà introdotta la tipologia di ponti in questione, seguentemente verranno proposti degli accenni teorici di supporto alla trattazione del fenomeno della fatica, e, in conclusione, verrà presentato e analizzato un caso studio conducendo le usuali metodologie di verifica a vita illimitata proposte dagli Eurocodici (www.masera-eg.it).
Lo stato dell’arte
L’impalcato da ponte in lastra ortotropa è costituito da una lamiera piana sottile irrigidita mediante nervature longitudinali (ribs) sorrette da travi trasversali (floorbeams) che presenta diversa rigidezza nelle due direzioni ortogonali (Figura 1).
Questo sistema costruttivo ha avuto origine in America nel 1930 dall’A.I.S.C. (American Institute of Steel Construction), che proponeva un nuovo approccio alla progettazione dei ponti con particolare attenzione alla loro leggerezza, realizzati completamente in acciaio.
Gli impalcati in lastra ortotropa in acciaio (OSD) sono stati ampiamente utilizzati in seguito alla Seconda Guerra Mondiale in ponti di grande luce per molti vantaggi come peso contenuto, alta resistenza, poche connessioni, durabilità, rapida costruzione ed economia del ciclo di vita [3].
Nonostante ciò, sono soggetti a danni di fatica in corrispondenza dei giunti saldati, in seguito al ripetuto transito veicolare e a causa della presenza di tensioni residue in corrispondenza delle saldature, che possono sostanzialmente condizionare la loro vita in servizio [4].
Il fenomeno della fatica nelle piastre ortotrope
Il fenomeno della fatica sui ponti in acciaio iniziò ad essere studiato a partire dagli anni Sessanta, quando molte strutture d’America e d’Europa manifestarono collassi strutturali con fratture da fatica.
Secondo le Norme ASTM [5], “la fatica è un processo permanente, progressivo e localizzato di cambiamento strutturale in un materiale soggetto a condizioni di tensione e deformazione variabili nel tempo e può portare alla formazione di cricche e/o alla frattura dopo un sufficiente numero di cicli”.
La vita di un elemento strutturale nei confronti della fatica si suddivide in tre fasi:
- nucleazione: periodo di vita del dettaglio fino alla formazione di un difetto superficiale a partire da un danneggiamento microscopico iniziale;
- propagazione stabile: aumento della dimensione del danneggiamento all’interno del materiale, in direzione ortogonale al campo tensionale applicato;
- collasso e rottura finale: in seguito alla propagazione della cricca, la sezione resistente non è più in grado di sopportare il carico applicato.
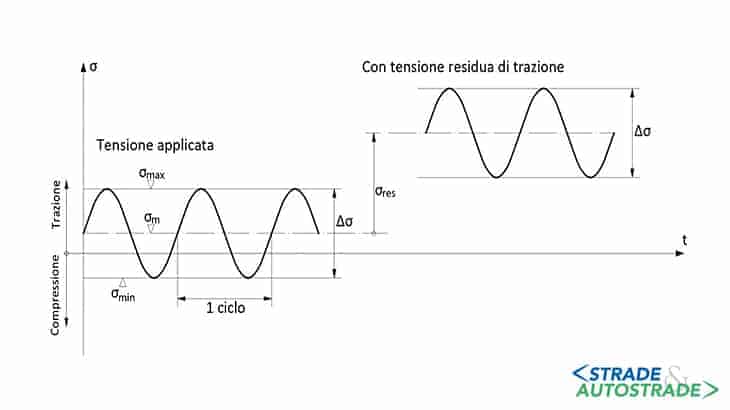
La tensione media ha un’influenza significativa nel comportamento a fatica, in quanto se di trazione tende a diminuire la resistenza a fatica mentre, se di compressione, ne aumenta il valore (Figura 2 sopra).
I danneggiamenti dovuti ai fenomeni di fatica nei ponti a piastra ortotropa possono essere potenzialmente causati da:
- difetti nelle saldature;
- vibrazione locale delle nervature e delle piastre;
- adozione di dettagli costruttivi poco adatti alla resistenza per fatica;
- esposizione ad ambiente corrosivo;
- sviluppo di difetti superficiali;
- insorgenza di tensioni secondarie non previste in sede di progetto.
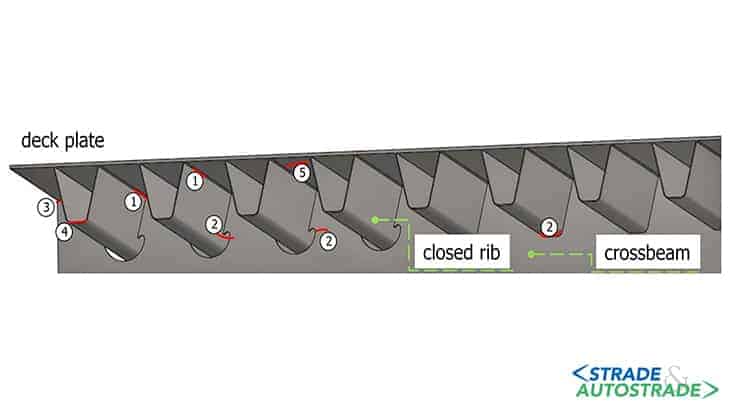
I carichi ciclici da traffico trasferiscono tensioni a una vasta quantità di punti critici della piastra ortotropa causando la rottura potenzialmente in corrispondenza di [6]:
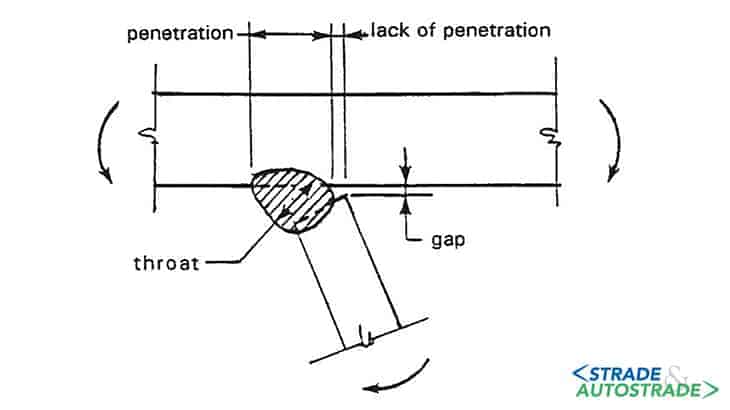
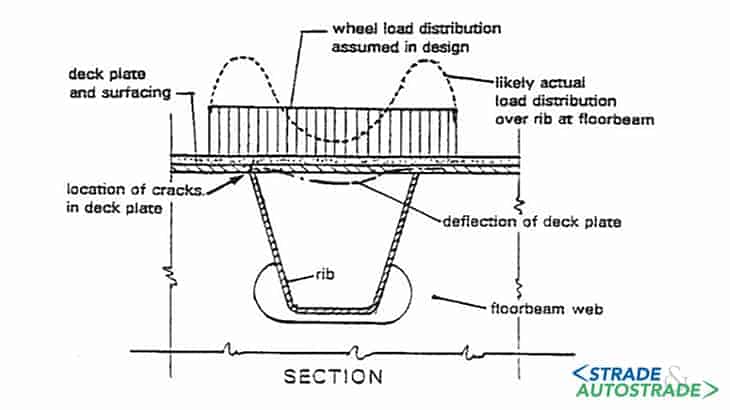
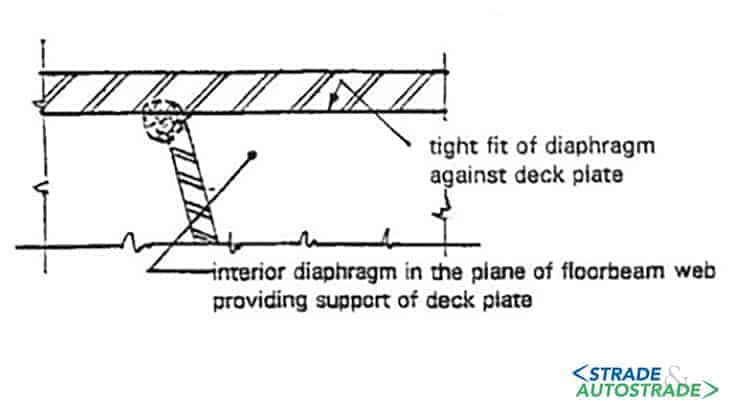
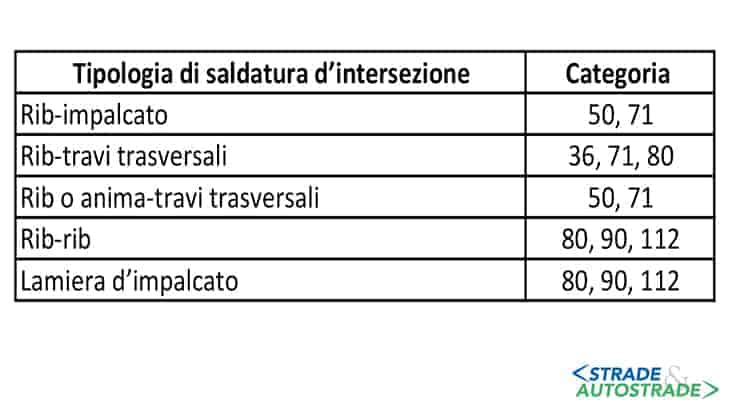
- saldature rib-impalcato: questa connessione è sollecitata particolarmente a flessione fuori piano (Figura 3 sopra);
- saldature rib-travi trasversali: la concentrazione di sforzi è causata principalmente dal transito veicolare;
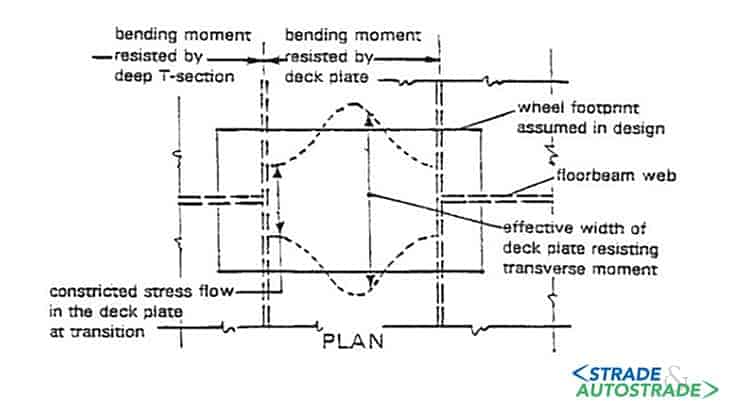
- saldature anima-travi trasversali: dove si osservano tensioni normali, tangenziali e flessionali nei due diversi piani (Figure 4A, 4B e 4C sopra).
Leggi/modelli per la valutazione della fatica
La curva di Wöhler
Le curve di Wöhler sono ottenute tramite prove di carico ciclico uniassiale ad ampiezza costante fino a rottura su provini vergini. Tali curve sono in scala bi-logaritmica e relazionano la variazione di tensione S (normale o tangenziale) con il numero di cicli che portano a rottura N (Figura 5).
Il criterio di danneggiamento lineare di Palmgreen-Miner
Viene definito il danneggiamento Di indotto dall’applicazione di un carico qualsiasi, ad ampiezza costante Si per un numero di cicli ni:
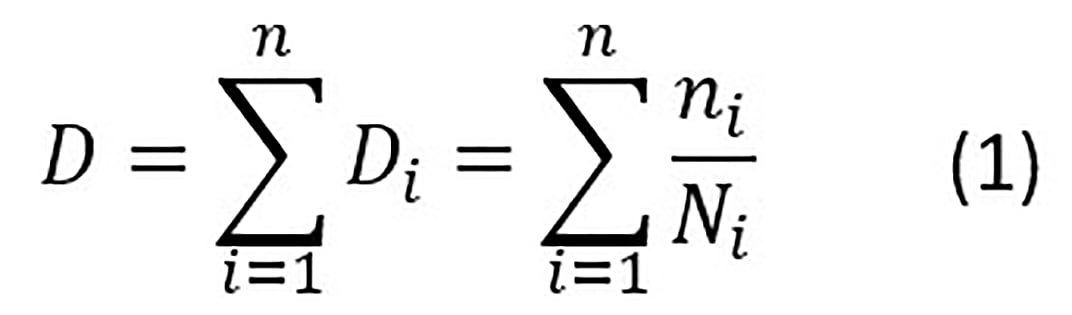
dove:
- ni = numero di cicli di ampiezza Δσ1,d = γMf · ΔσMAX indotti dallo spettro di carico;
- Ni = numero di cicli, di ampiezza Δσ1,d, che porterebbe a rottura, ricavato dalla curva S-N di Normativa caratteristica del dettaglio oggetto di verifica.
Se 0 < Di < 1 il dettaglio è danneggiato, mentre se Di ≥ 1 si verifica la rottura per fatica.
Il danneggiamento Di cresce linearmente con l’aumentare del numero di cicli Ni che portano a rottura.
L’approccio normativo
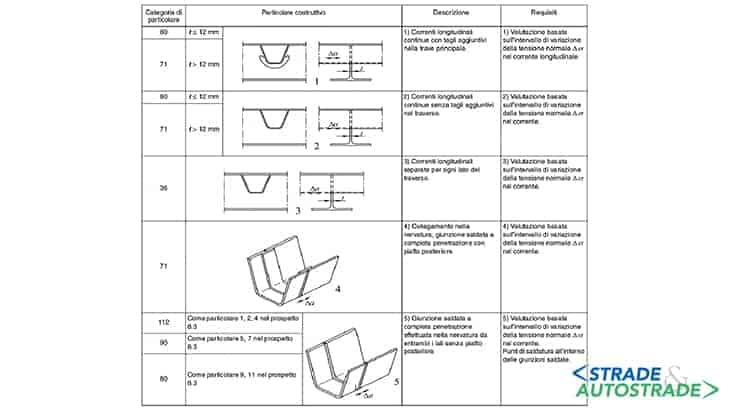
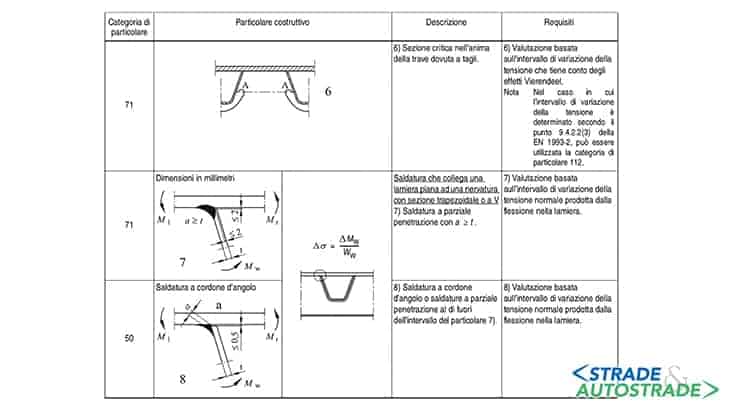
I giunti saldati possono essere categorizzati in funzione degli elementi collegati. L’Eurocodice EN1993-1-9 [7] associa a ogni tipo di giunto una categoria e una resistenza caratteristica, come segue nelle Figure 7 e 8.
Per verificare la resistenza a fatica nella pratica, viene assegnato lo spettro di carico che fornisce il numero di ripetizioni di ciascun livello delle azioni di progetto in un intervallo di tempo di riferimento, in funzione della destinazione d’uso della struttura e dell’intensità di utilizzo.
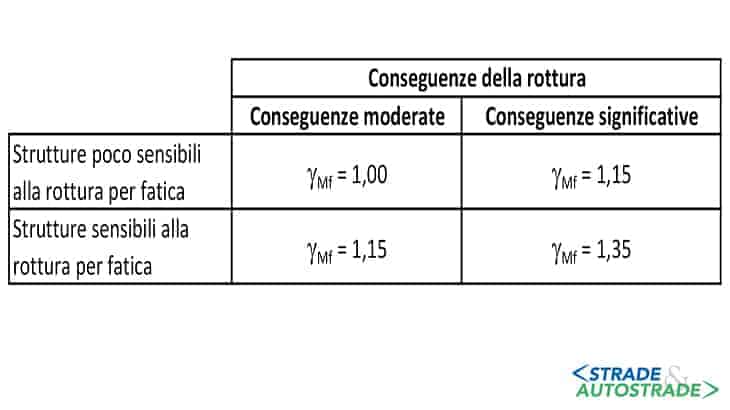
Per le verifiche si identifica la massima variazione di tensione di progetto Δσ1,d moltiplicando lo spettro di tensione Δσ1 per il coefficiente parziale di sicurezza per verifiche a fatica γMf.
Le curve S-N di norma
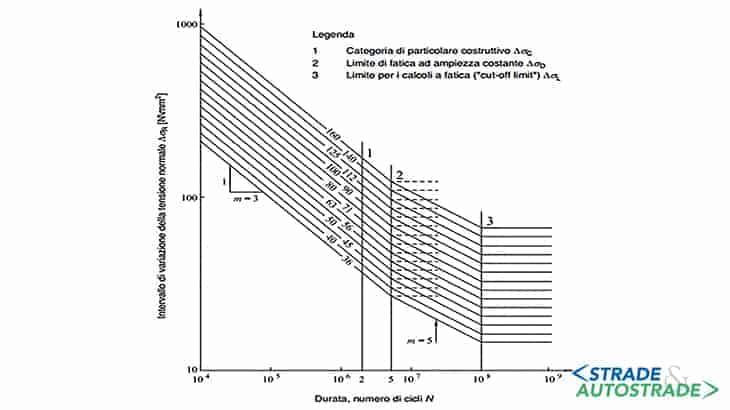
In funzione della geometria dell’elemento e del tipo di saldatura, al §5.1.4.3 delle NTC [8] e al §7.1 delle UNI EN 1993-1-9 [7] vengono riportate le curve che indicano la tensione di resistenza (normale o tangenziale) in scala bi-logaritmica.
Per ogni categoria di dettaglio costruttivo, la curva S-N per N = 2 · 106 [cicli] rappresenta la resistenza a fatica ΔσR o ΔτR [N/mm2] (Figura 10).
L’equazione della curva S-N per tensioni normali è definita a tratti:
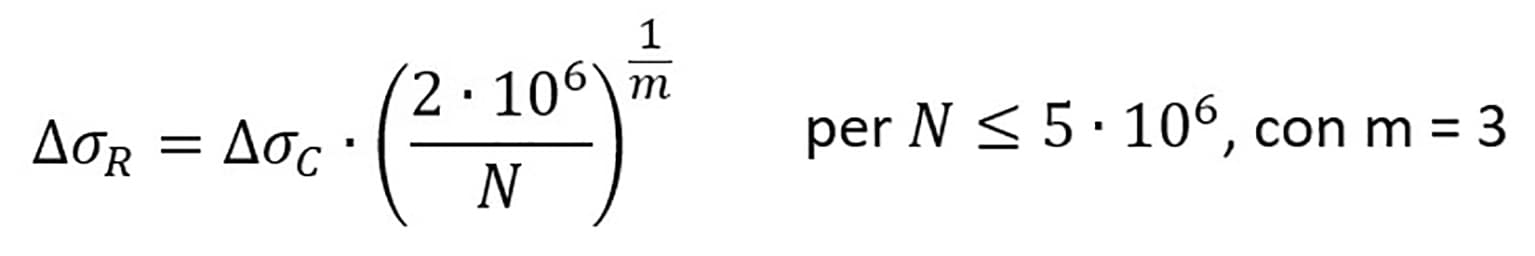
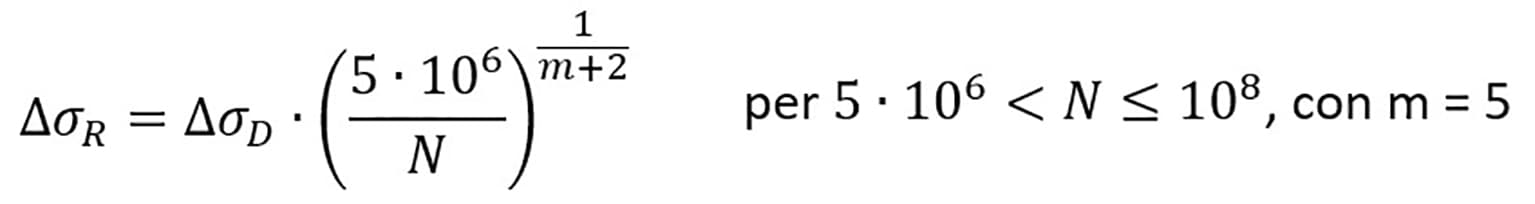
dove:
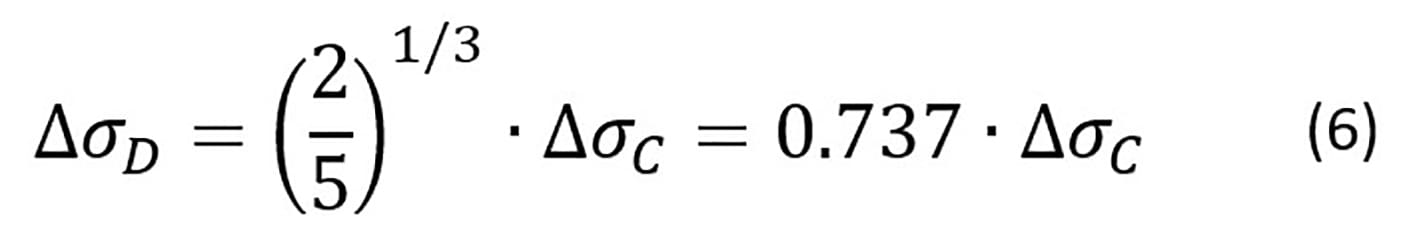
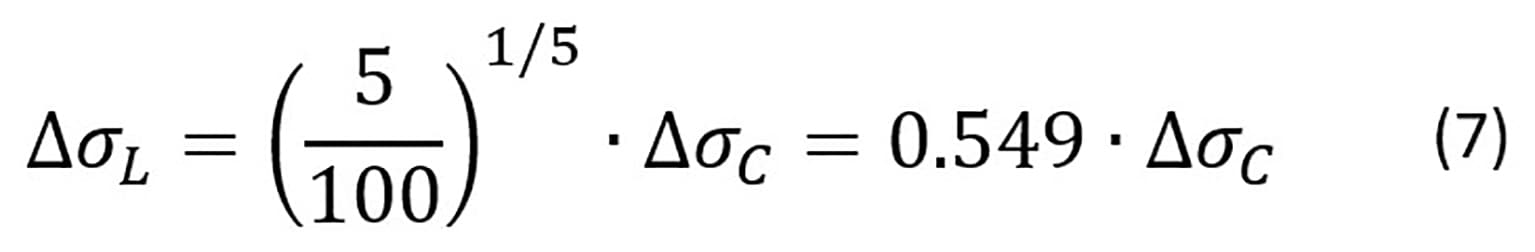
Le verifiche a vita illimitata
Vengono condotte verifiche a fatica per Vita illimitata, considerando la massima variazioni di tensione, ΔσMAX = | σMAX – σMIN |, indotte nel dettaglio dallo spettro di carico Modello di carico di fatica 2 controllando che risulti minore del limite di fatica del dettaglio stesso:
dove:
- ΔσMAX,d = valore di progetto delle massime variazioni di tensione normale indotte nel dettaglio;
- ΔσD = limite di resistenza a fatica ad ampiezza costante.
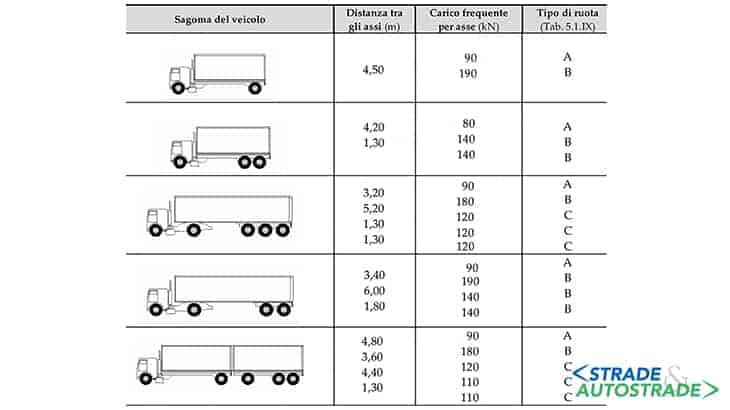
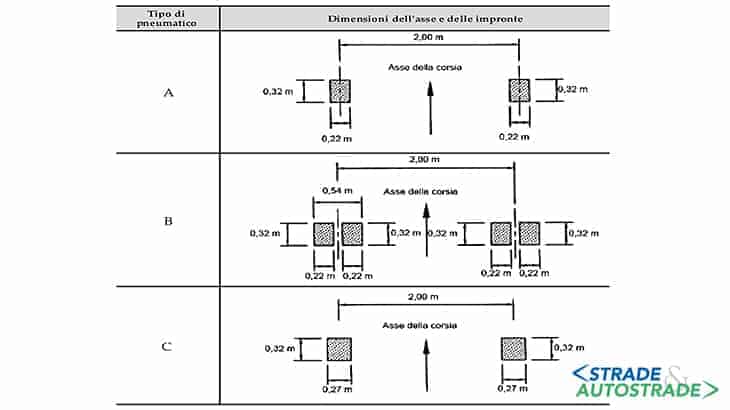
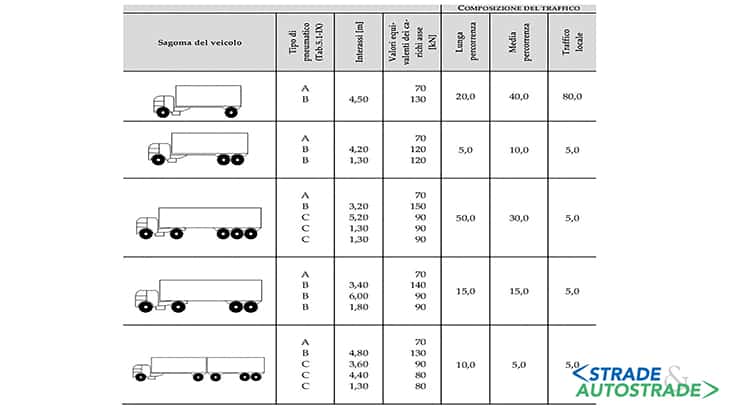
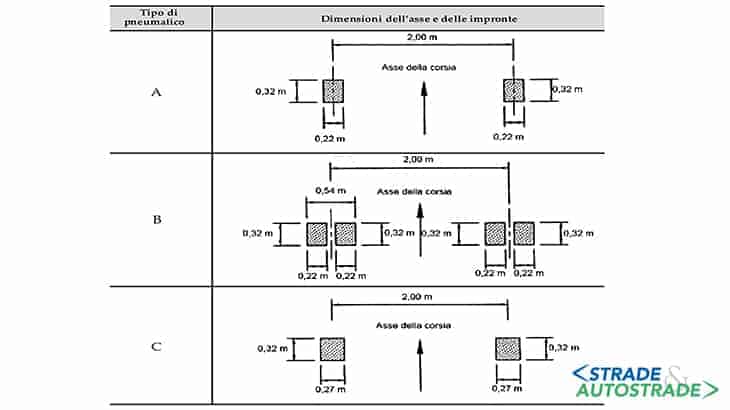
Questo modello di carico a fatica è costituito da un set di cinque autocarri idealizzati definiti mediante la disposizione degli assi e carichi frequenti per assi Qki (Figure 11 e 12) posizionati nella corsia lenta (Figura 16 più avanti).
Si prende in considerazione la sagoma che produce sul dettaglio le massime variazioni di tensione.
Le verifiche a danneggiamento
È necessario controllare che il danneggiamento indotto dallo spettro di tensione del Modello di carico di fatica 4, valutato mediante la legge di Palmgren-Miner, risulti D ≤ 1 (Figure 13 e 14).
Bibliografia
[1]. Troitsky e S. Michael, Orthotropic bridges-theory and design, 1987.
[2]. R. Connor, J. Fisher, W. Gatti, V. Gopalaratnam, B. Kozy, B. Leshko, D. McQuaid, R. Medlock, D. Mertz, T. Murphy, D. Paterson, O. Sørensen, J. Yadlosky – “Manual for design, construction, and maintenance of orthotropic steel deckbridges”, Washington, D.C., USA, Federal Highway Administration, 2012.
[3]. Z. Qian, D. Abruzzese – “Fatigue failure of welded connections at orthotropic bridges”, Frattura ed integrità strutturale, p. pp. Pages 105-112, 2009.
[4]. Q. Zhang, Y. Liu, D. J. Yi Bao, Y. Bu, Q. Li – “Fatigue performance of orthotropic steel-concrete composite deck with large-size longitudinal U-shaped ribs”, Engineering Structures, vol. Volume 150, pp. 864-874, 2017.
[5]. ASTM American National Standard, ANSI/ASTM, E206-72, 1979.
[6]. R. Wolchuk – “Steel Orthotropic Decks: Developments in the 1990s”, Transportation Research Record, vol. 1688, n° 1, pp. 30-37, 1999.
[7]. Eurocodice 3 – Progettazione delle strutture di acciaio, Parte 1-9 (UNI EN 1993-1-9): Fatica, anno 2005.
[8]. Ministero delle Infrastrutture e dei Trasporti, Decreto Ministeriale 17 Gennaio 2018 “Norme Tecniche per le Costruzioni”.
La seconda parte dell’articolo è sul fascicolo n° 149 Settembre/Ottobre 2021 a pag. 57 e online su https://www.stradeeautostrade.it/ponti-e-viadotti/il-fenomeno-della-fatica-nei-ponti-in-acciaio-a-lastra-ortotropa-seconda-parte/.
> Se questo articolo ti è piaciuto, iscriviti alla Newsletter mensile al link http://eepurl.com/dpKhwL <